Concavité / Convexité

Mathias André M1 EPP 2009
École Polytechnique – Crest
Concavité / Convexité
Résumé de cours
1 Définitions
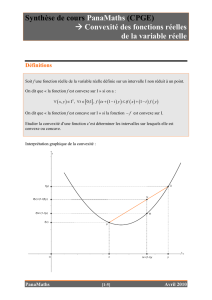
Définition 1.1 On dit qu’une fonction fest convexe sur un intervalle Isi et seulement si :
∀(x1, x2)∈I2,∀λ∈[0,1], f(λx1+ (1 −λ)x2)≤λf(x1) + (1 −λ)f(x2)
On dit qu’une fonction fest concave sur un intervalle Isi et seulement si −fest convexe.
Les cas stricts correspondent aux mêmes définitions avec des inégalités strictes pour 0<λ<1.
fest convexe signifie que la droite qui relie f(x1)àf(x2)est au-dessus de la courbe représentative
de fsur [x1, x2], autrement dit que fest au-dessus de ses tangentes (si elles existent).
Définition 1.2 On dit qu’une fonction fest quasi-convexe sur un intervalle Isi et seulement si :
∀(x1, x2)∈I2,∀λ∈[0,1], f(λx1+ (1 −λ)x2)≤max{f(x1), f(x2)}
On dit qu’une fonction fest quasi-concave sur un intervalle Isi et seulement si −fest quasi-convexe 1.
Les cas stricts correspondent aux mêmes définitions avec des inégalités strictes pour 0<λ<1.
fest quasi-convexe sur Iest ainsi équivalent à
∀(x1, x2)∈I2,∀λ∈[0,1], f(x1)≤f(x2)⇒f(λx1+ (1 −λ)x2)≤f(x2)
Intuitivement, une fonction qui est décroissante puis croissante est quasi-convexe 2.
Les graphiques ci-dessous donnent une représentation de ces définitions.
MAT2.3
sur les notions de concavité et de convexité des fonctions.
Définition:
Une fonction f(x) est une fonction convexe si, pour tous points x1, x2 de son domaine et pour tout
, 1 < < 0 ,
λ
λ
. )
x
( f ) - 1 ( + )
x
( f )
x
) - 1 ( +
x
( f2 1 2 1
λ
λ
λ
λ
≤
(Une fonction est strictement convexe si la dernière inégalité est stricte, à savoir,
)
x
( f ) - 1 ( + )
x
( f < )
x
) - 1 ( +
x
( f2121
λ
λ
λ
λ
et )
x x
21
≠
.
Similairement, une fonction concave est définie de la même manière mais le sens de l'inégalité est
renversé.
Exemples:
x1
λ
x1 + (1 -
λ
)x2 x2
f(x1)
f(x2)
f(x)
x
x1 λx1 + (1 - λ)x2 x2
x
f(x1)
f(x2)
f(x)
λf(x1)+(1-λ)f(x2)
f(
λ
x1+(1-
λ
)x2)
f(λx1+(1-λ)x2)
λ
f(x1)+(1-
λ
)f(x2)
Fonction convexe Fonction concave
1. Ne pas oublier que max−f=−minf.
2. C’est une propriété assez large, il y a donc « beaucoup » de fonctions quasi-convexes en économie. Ainsi, la plupart
des fonctions d’utilité « classiques » en économie le sont.
1

MAT2.5
Exemples:
• DIFFÉRENTIELLE TOTALE
Soit . ) x ( f =y
Alors dx ) x ( ’ f =dy est la différentielle totale et on a y dy
∆
≠
, i.e. dy est une approximation de
.
)
x
(
f
-
)
x
+
x
(
f
=
y
∆
∆
x1
λ
x
1
+ (1
-
λ
)x
2
x2
f(x1)
f(λx1 + (1 - λ)x2)
f(x2)
f(x)
x
x1
λ
x
1
+ (1
-
λ
)x
2
x2
x
f(
λ
x1 + (1 -
λ
)x2)
f(x1)
f(x2)
f(x)
Fonction Quasi Concave Fonction pas Quasi Concave
Afin de distinguer convexe et quasi-convexe, considérons la fonction partie entière définie sur Rpar
x7→ xxyoù xxyest le plus grand entier plus petit que x. C’est une fonction en escalier constante sur les
intervalles de la forme [n, n+1[ où n∈Nqui est quasi-convexe mais pas convexe (remarquer l’importance
des discontinuités).
Voilà enfin une définition moins fondamentale mais qui peut s’avérait être utile :
Définition 1.3 On dit qu’un ensemble Eest convexe si et seulement si
∀(x1, x2)∈E2,∀λ∈[0,1], λx1+ (1 −λ)x2∈E
Intuitivement, cela signifie que si l’ensemble contient deux points, il contient le segment qui les relie 3.
Cette définition est utile pour interpréter la propriété de convexité des préférences qui se traduit par le
fait que tout panier de bien faiblement préféré est convexe.
2 Premières propriétés et applications
On se contentera de donner quelques propriétés dans le cas convexe, pour fconcave il suffit de les
traduire avec g=−f. Se reporter à un cours de maths pour plus de détails et des démonstrations.
ëSî fest dérivable sur I, alors fconvexe si et seulement si f0croissante sur I. Sî fest deux fois
dérivable sur I, alors fconvexe si et seulement si f00 positive sur I.
ëLemme des trois pentes :
fconvexe si et seulement si ∀(x, y, z)∈I3, x < y < z ⇒f(y)−f(x)
y−x≤f(z)−f(y) z−y
ëInégalité de Jensen :
Si fconvexe sur Iet (x1, . . . , xn)∈In,(λ1, . . . , λn)∈[0,1]ntels que Pn
i=1 λi= 1, alors
f n
X
i=1
λixi!≤
n
X
i=1
λif(xi)
ëUne somme pondérée de fonctions convexes est convexe. Une borne supérieure de fonctions convexes
est convexe. Si f(.)est convexe, x7→ f(ax +b)l’est.
ëToute fonction convexe est quasi-convexe. Toute fonction monotone est quasi-convexe.
ëLes fonctions quasi-convexes sont caractérisées par la convexité des ensembles de niveau : fquasi-
convexe sur Isi et seulement si ∀α∈R,{x∈I, f (x)≤α}est un ensemble convexe.
cf. microéconomie, Utillité et convexité des préférences : Si on considère des préférences sur
un ensemble X, une représentation numérique de ces préférences peut être donnée par toute fonction
Uavec le domaine Xet l’image dans Rtelle que xy⇔U(x)> U (y). Supposons que Usoit une
représentation numérique des préférences , c’est-à-dire une fonction d’utilité. Alors Uest quasi-concave
si et seulement si les préférences sont convexes ; Uest strictement quasi-concave si et seulement si les
préférences sont strictement convexes (application de la dernière propriété).
3. Faire un dessin et remarquer que l’ensemble est assez « rond ».
2