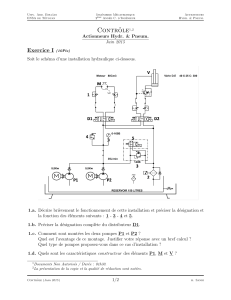
Projet Mathématiques Ingénieur EPO : Distributions, Fonctions Spéciales, NURBS

Projet de Math´ematique pour Ing´enieur
Ecole Polytechnique de Ouagadougou (EPO)
Sujet 4
Groupe 4 : A completer avec les noms des
membres du groupe
7 avril 2025
R´esum´e Les notions pr´esent´ees dans ces projets constituent des outils math´ematiques
essentiels pour les sciences et techniques de l’ing´enieur.
La th´eorie des distributions fournit un cadre rigoureux pour mod´eliser des
ph´enom`enes non classiques, tels que les impulsions ou discontinuit´es, fr´equemment
rencontr´es dans le traitement du signal, les syst`emes dynamiques et la m´ecanique.
Les fonctions sp´eciales, quant `a elles, interviennent comme solutions naturelles
d’´equations diff´erentielles fondamentales. Leur connaissance facilite l’analyse de
nombreux ph´enom`enes physiques, notamment en vibration, en thermodynamique
et en ´electromagn´etisme.
Enfin, les courbes et surfaces de B´ezier jouent un rˆole central dans la mod´elisation
g´eom´etrique. Leur utilisation est courante en conception assist´ee par ordinateur
(CAO), robotique, et graphisme, o`u pr´ecision, souplesse et contrˆole sont requis.
La maˆıtrise de ces outils permet `a l’ing´enieur de passer efficacement de la
mod´elisation math´ematique `a l’analyse et `a la mise en œuvre de solutions concr`etes,
dans un cadre multidisciplinaire.
Keywords Th´eorie de Distribution ·Fonctions Sp´eciales ·Courbes de BEZIER ·
CAO
G´enie M´ecanique 1 (GM1)
S. SANOGO
Ecole Polytechnique de Ouagadougou (EPO)
B: [email protected]

2 Groupe 4 : A completer avec les noms des membres du groupe
1 Th´eorie de Distribution
1. Pour toute fonction φ∈ D, on consid`ere une application Tsur D, d´efinie par :
⟨T, φ⟩= lim
n→+∞ n
X
k=1
φ1
k−nφ(0) −nφ′(0) ln(n)!.(1)
(a) Prouver que cette applicaton existe et qu’elle est une distribution sur R.
(b) Quelle est son ordre ?
Exercice 1 GM1–2024-2025
2 Fonctions Sp´eciales
On consid`ere les fonctions Gamma Γ, et Beta Bpar :
Γ(x) = Z+∞
0
tx−1e−tdt (2)
B(x, y) = Z1
0
tx−1(1 −t)y−1dt (3)
1. Donner des applications de chacune des ces deux fonctions dans le domaine
des sciences et techniques de l’ing´enieur.
2. Etudier Γ, puis repr´esenter sa courbe dans un rep`ere orthogonal du plan.
3. D´emontrer que : ∀x, y > 0
B(x, y) = Γ(x)Γ(y)
Γ(x+y)(4)
Γ(2x) = 22x−1
√πΓ(x)Γx+1
2(5)
4. D´emontrer que :
Γ(x)Γ(1 −x) = π
sin(πx).(6)
Exercice 2 GM1–2024-2025

Sujet 4 Math pour Ing. 3
3 Courbes de BEZIER, Initiation aux NURBS & application `a la CAO
1. D´efinissez ce qu’est une courbe NURBS.
2. Comparez les courbes NURBS aux courbes polynomiales classiques (Bezier,
B-spline).
3. Justifier, pourquoi les NURBS sont-ils plus adapt´es `a l’industrie automobile ?
4. Mod´elisation d’une pi`ece automobile
(a) Donner trois pi`eces d’une automobile dont la g´eom´etrie peut ˆetre mod´elis´ee
`a l’aide de NURBS.
(b) Pour l’une d’elles, d´ecrivez comment on peut passer d’un croquis initial `a
un mod`ele 3D avec NURBS dans un logiciel de CAO.
(c) Faite un illustration avec un programme MATLAB.
Exercice 3 GM1–2024-2025
4 Consigne `a Suivre :
4.1 R´epondre rigoureusement `a toute les Questions. Les questions qui concernes
les application contr`etes doivent ˆetre justifi´e par des exemples et des r´ef´erences
Bibliographiques.
4.2 La rapport de ce projet doit ˆetre r´edig´e avec L
A
T
E
X.
4.3 Vous devez en fichier.zip l’ensemble des documents r´esultats de votre projet
(le pr´esent sujet, votre rapport en pdf, .tex, toutes les images, codes matlab, etc)
4.4 Date limite d’envoie : 30 Avril 2025 par email : [email protected]
4.5 Il y a aura une deuxi`eme phase de pr´esentation des projets (dur´ee : 10 min).
Date sera d´efinie avec le Chef de Departement.
Bonne Chance et Beaucoup de Courage `a Tous.