Exercices d'Électrostatique : Champs et Potentiels

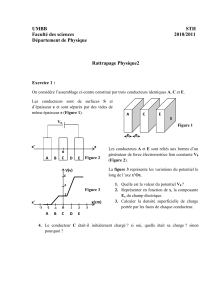
1
T
Tr ra av va au ux x D Di ir ri ig gé és s : : E El le ec ct tr ro os st ta at ti iq qu ue e
Département de Physique
E
Ex xe er rc ci ic ce e
1
1
:
: On considère deux charges électriques ponctuelles q et -4q , distantes
de a . q étant positif .
a. Déterminer le champ
E
en un point M tel que
ixOM 
. Dessiner les
champs créés par chacune des charges et le champ résultant.
b. Déterminer la valeur de x négatif pour laquelle
0 E
. Donner la valeur
du potentiel électrique V en ce point.
E
Ex xe er rc ci ic ce e 2 2 : : On considère une boucle de rayon R portant une charge électrique de
densité linéique uniforme λ. Soit M un point de l'axe de la boucle d'abscisse z .
a. Déterminer directement :
 le champ électrique
)(zE
 le potentiel
)(zV
(on prendra
0V
pour z infini).
b. Retrouver l'expression du champ électrique à partir de celle du potentiel.
E
Ex xe er rc ci ic ce e 3 3 : : Effectuer le calcul du champ électrostatique
E
crée par un disque de
rayon R portant la charge surfacique
cte
, en un point de son axe
) ;( kO 
. Tracer
E(z) en fonction de z .
kzOM 
. En faisant tendre R vers l'infini, en déduire le
champ créé par un plan (infini) de charges.
E
Ex xe er rc ci ic ce e 4 4 : : On considère une demi-droite
)j ;(  A
portant une densité linéique de
charges uniforme . Déterminer le champ en M. Avec
jaOA 
;
ixOM 
.
) , ;( jiO 
étant un repère orthonormé.
E
Ex xe er rc ci ic ce e 5 5 : : Par application du théorème de Gauss, déterminer le champ en tout
point M de l'espace dans les cas suivants :
www.al3abkari-pro.com

2
1. une sphère de centre O de rayon R portant une densité surfacique de
charges uniforme .
2. une sphère de centre O de rayon R portant une densité volumique de
charges uniforme .
3. une distribution de charges à symétrie sphérique centrée en O telle qu’à
une distance r de O ,
kr
e 0
.
4. un cylindre de longueur infinie, de rayon R, portant une densité
surfacique uniforme .
5. un cylindre de longueur infinie, de rayon R, portant une densité
volumique de charges r uniforme .
E
Ex xe er rc ci ic ce e 6 6 : : On considère deux sphères conductrices, l’une notée S1, pleine et
portant une charge Q1 négative. L’autre, S2, creuse et ne portant aucune charge.
a. Donner la répartition des charges sur S2, lorsqu’on place S1 à l’intérieur de
S2.
b. Donner la nouvelle répartition des charges lorsqu’on établi un contact
électrique entre les deux sphères.
c. En plus du contact électrique entre S1 et S2, on relie S2 au sol. Quelle est
alors, la nouvelle répartition des charges?
E
Ex xe er rc ci ic ce e 7 7 : : On considère deux sphères S et S’ de rayons R et R’ portant des
charges respectives Q et Q’ et reliées par un fil conducteur dont on néglige la
charge. Les deux sphères sont supposées suffisamment éloignées pour que leurs
charges restent uniformes.
a. Etablir une relation entre les champs E et E’ , au voisinage de chaque
sphère, et leurs rayons. Ce résultat est-il prévisible?
b. Examiner le cas particulier où S représente le globe terrestre
( R=6400km ).
E
Ex xe er rc ci ic ce e 8 8 : : Calculer la capacité d’un condensateur dont l’armature interne est un
cylindre d’axe Δ , de rayon R1 et dont la surface interne de l’armature externe est un
cylindre de même axe Δ et de rayon R2 (condensateur cylindrique). On calculera la
capacité pour une longueur h du condensateur.
Calculer le cas où R1 et R2 sont peu différents. On supposera R2 = R1 + e , avec e<< R1
et R2.
www.al3abkari-pro.com

S
Sé ér ri ie e n n° ° 1 1 : : C Co or rr ri ig gé é
E
Ex xe er rc ci ic ce e 1 1 : :
a/ Selon la position relative du point M,
on distingue 3 cas :
1er cas :
xa 
ixEi
axx
axaxq
i
ax
q
x
q
E
)(
)(
)3)((
4
)
)(
4
(
41
22
0
22
0
Comme
ax 
, on s’aperçoit que
0)( xE
2eme cas :
ax 0
ixEi
axx xaaxq
i
xa q x
q
E
)(
)( )3)((
4
)
)( 4
(
41
22
0
22
0
Dans ce cas, E(x) peut être :
positif (
3
a
x
), négatif (
3
a
x
) ou nul (
3
a
x
)
3eme cas :
0x
ixEi
axx
xaaxq
i
xa
q
x
q
E
)(
)(
)3)((
4
)
)(
4
(
41
22
0
22
0
Comme
x0
, on a
03  xa
Dans ce cas, E(x) peut être :
positif (
ax 
), négatif (
ax 
) ou nul (
ax 
)
b/
0)( aE
a
q
a
q
a
q
aV
00 4
)
2
4
(
41
)(
E
Ex xe er rc ci ic ce e 2 2 : :
Calcul direct du champ :
La symétrie du problème impose
que :
zEd 
//
z
u
a
M
x
Q1 Q2
q -4q
O
www.al3abkari-pro.com

Le champ créé en M par une longueur
infinitésimale de longueur R dφ au
point P de coordonnées p po ol la ai ir re es s ( (R R, ,
φ
φ
)
) v va au ut t : :
A
Av ve ec c : :
22 zRr 
. En réalité, la seule
composante utile de
Ed 
est la
composante suivant
z
, comme le
champ final
E
est suivant
z
.
On projette
Ed 
sur l’axe (O, z) :
Le champ total est :
2
0
2
0
2
0
cos
4
cos
4
)( d
r
R
d
r
R
zE boucle
car α et r sont constants lorsque le
point P décrit la boucle. Soit,
2
0
cos
2
)( r
R
zE
En revenant aux données de
l’exercice :
2/322
0)(
2
)( Rz zR zE 
Remarque : E(z) = -E(-z) (à cause de
la symétrie)
Calcul direct du potentiel :
On applique la définition :
On suppose que l’origine des
potentiels est à l’infini.
2
0
000 44 1
41d r
R
r
Rd
r
dq
Vboucleboucle
Soit finalement :
22
0
2Rz
R
V
On peut retrouver ce résultat à
partir de la relation :
VgradE 
.
Comme E ne dépend que de z, il
vient :
z
V
zE  )(
, soit en dérivant
l’expression de E(z) :
2/322
0)(
2
)( Rz zR zE 
E
Ex xe er rc ci ic ce e 3 3 : : On calcule le champ par
la méthode directe pour un point M
de cote z positive :
zz u
r
Rd
u
rdl
Ed 
2
0
2
041
41
cos
412
0r
Rd
dEdE z
www.al3abkari-pro.com

 Tout plan contenant (Oz) est
plan de symétrie de la
distribution, donc pour tout
point M de (Oz), est
suivant
 On utilise comme surface
élémentaire une couronne
élémentaire de rayon r ,
d' épaisseur dr . Cette
couronne est vue sous un angle
α depuis le point M. On
intégrera suivant α pour
« balayer » toute la surface
de la couronne.
 La surface de cette couronne
élémentaire est
. Le champ créé
en M par cette couronne
élémentaire est donc
 Comme on veut intégrer
suivant α, on va chercher à
tout exprimer en fonction de
α et z :
o donc
o
 On obtient finalement
, ce qui après simplification
donne
 On intègre pour entre 0 et
:
 On revient aux données du
problème :
 La symétrie de la distribution
par rapport au plan du disque
assure
 On peut considérer que le plan
est un disque de rayon infini :
z
RuME 
0
2
)(
lim
E
Ex xe er rc ci ic ce e 5 5 : : 1. Sphère chargée en
surface avec,
cte
Fait lors de la séance du cours.
www.al3abkari-pro.com