Exercices Corrigés : Polynôme Second Degré

Chapitre 1 : Polynôme du second degré
POLYNÔME DU SECOND DEGRÉ
CORRECTION DES EXERCICES
INÉQUATIONS DU SECOND DEGRÉ:
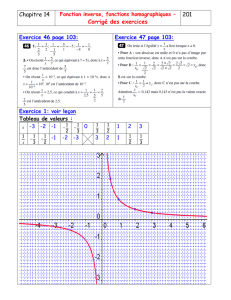
Exercice 1 :
Résolvons dans Rles inéquations suivantes sans utiliser le discriminant.
1. (2x+ 1)(x−3) >0
Posons (2x+ 1)(x−3) = 0
(2x+ 1)(x−3) = 0 ⇔2x+ 1 = 0 ou x−3=0
⇔x=−1
2ou x= 3
Faisons un tableau de signe:
x
2x+ 1
x−3
(2x+ 1)(x−3)
−∞ −1
23+∞
−0+ +
− − 0+
+0−0+
Ainsi, pour tout x∈−∞,−1
2∪]3,+∞[on a (2x+ 1)(x−3) >0.
Par conséquent, l’ensemble solution de l’inéquation est l’intervalle:
−∞,−1
2∪]3,+∞[
c
Cours Galilée Toute reproduction, même partielle, est strictement interdite. 1

Chapitre 1 : Polynôme du second degré
2. 4x≥2 + x2
4x≥2 + x2⇔ −x2+ 4x−2≥0⇔x2−4x+ 2 ≤0
Posons x2−4x+ 2 = 0
x2−4x+ 2 = 0 ⇔(x−2)2−4 + 2 = 0
⇔(x−2)2−2=0
⇔(x−2)2= 2
⇔x−2 = √2ou x−2 = −√2
⇔x= 2 + √2ou x= 2 −√2
Faisons un tableau de signe.
x
x2−4x+ 2
−∞ 2−√2 2 + √2+∞
+0−0+
Ainsi, x2−4x+ 2 ≤0pour tout x∈2−√2,2 + √2
Par conséquent, l’ensemble solution de l’inéquation est l’intervalle:
2−√2,2 + √2
3. 16 −(x−4)2≤0
Posons 16 −(x−4)2= 0
16 −(x−4)2= 0 ⇔42−(x−4)2= 0
⇔(4 −x+ 4)(4 + x−4) = 0
⇔x(8 −x)=0
⇔x= 0 ou x= 8
Faisons un tableau de signe:
c
Cours Galilée Toute reproduction, même partielle, est strictement interdite. 2

Chapitre 1 : Polynôme du second degré
x
16 −(x−4)2
−∞ 0 8 +∞
−0+0−
Ainsi, 16 −(x−4)2≤0pour tout x∈]−∞,0] ∪[8,+∞[
Par conséquent, l’ensemble solution de l’inéquation est l’intervalle:
]−∞,0] ∪[8,+∞[
4. −√5(2x−1)2≤0
On sait que pour tout x∈R,(2x−1)2≥0
Ce qui équivaut à −√5(2x−1)2≤0car −√5<0
Par conséquent Rest l’ensemble solution de l’inéquation.
5. −2x2<5x
−2x2<5x⇔ −2x2−5x < 0
Posons −2x2−5x= 0
−2x2−5x= 0 ⇔ −x(x+ 5) = 0
⇔x= 0 ou x+ 5 = 0
⇔x= 0 ou x=−5
Faisons un tableau de signe:
x
−2x2−5x
−∞ −50+∞
−0+0−
Ainsi,−2x2−5x < 0pour tout x∈]−∞,−5[ ∪]0,+∞[
Par conséquent, l’ensemble solution de l’inéquation est l’intervalle:
]−∞,−5[ ∪]0,+∞[
c
Cours Galilée Toute reproduction, même partielle, est strictement interdite. 3

Chapitre 1 : Polynôme du second degré
6. 2x2−√2x > 0
Posons 2x2−√2x= 0
2x2−√2x= 0 ⇔x(2x−√2) = 0
⇔x= 0 ou 2x−√2=0
⇔x= 0 ou x=√2
2
Faisons un tableau de signe:
x
2x2−√2x
−∞ 0√2
2+∞
+0−0+
Exercice 2 :
On considère les fonctions fet gdéfinies sur Rpar :
f(x)=2x2−(3 + √2)x+ 6√2et g(x) = −x2+ 3x−2.
1. Déterminons les racines des fonctions fet gdans R.
•f(x)=2x2−(3 + √2)x+ 6√2
Soit ∆1le discriminant de l’équation 2x2−(3 + √2)x+ 6√2=0
∆1=b2−4ac
= [−(3 + √2)]2−4(2)(6√2)
= 9 + 6√2+2−48√2
= 11 −42√2
On sait que 11 <42√2donc 11 −42√2<0ainsi ∆1<0
∆1<0donc l’équation n’admet pas de solutions réelles.
Par conséquent, la fonction fn’admet pas de racines réelles.
c
Cours Galilée Toute reproduction, même partielle, est strictement interdite. 4

Chapitre 1 : Polynôme du second degré
•g(x) = −x2+ 3x−2
Soit ∆2le discriminant de l’équation −x2+ 3x−2=0
∆2=b2−4ac
= 32−4(−1)(−2)
= 9 −8
= 1
∆2>0donc l’équation admet deux solutions réelles distinctes:
x1=−b−√∆2
2a=−3−1 −2= 2 et x2=−b+√∆2 2a=−3 + 1 −2= 1
Par conséquent, la fonction gadmet deux racines distinctes: 1et 2
2. Donnons le tableau de signes des fonctions fet g.
•Tableau de signe de f
x
f(x)
−∞ +∞
+
•Tableau de signe de g
x
g(x)
−∞ 1 2 +∞
−0+0−
3. Déduisons l’ensemble solutions des inéquations f(x)<0et g(x)≤0
dans R.
•Solution de l’inéquations f(x)<0
A partir du tableau de signe de fprécédent on a:
c
Cours Galilée Toute reproduction, même partielle, est strictement interdite. 5