Cours S2 - Trigonométrie

_________________________________________________________________________________________________
Cours S1 : Trigonométrie Page 1 sur 4
Seconde – Lycée Desfontaines – Melle
Cours S2 - Trigonométrie
I. Préambule
1- Longueur d’un arc
Soit C un cercle de centre O et de rayon 1.
La longueur du cercle C est égale à 2π et son angle plein mesure 360°. La longueur du demi-cercle est
égale à π et l’angle plat mesure 180°.
Soient I et M deux points du cercle alors la mesure en degrés de l’angle Æ IOM est alors proportionnelle à
la longueur de l’arc È IM qu’il intercepte.
Sachant qu’un angle de 180° intercepte un arc de C de longueur π, on déduit le tableau de
proportionnalité suivant :
Mesure en degré 180 α
Longueur de l’arc intercepté π
l
D’où le tableau suivant
Mesure en degré de l’angle au centre 360° 180° 90° 60° 45° 30°
Longueur de l’arc intercepté
2- Cercle trigonométrique
Pour parcourir un cercle, on dispose de deux sens possibles : le sens des aiguilles d’une montre et le sens
inverse.
Par convention, on appelle sens direct ou sens positif, le sens inverse des aiguilles d’une montre.
On appelle cercle trigonométrique, un cercle de rayon 1 orienté dans le sens direct.
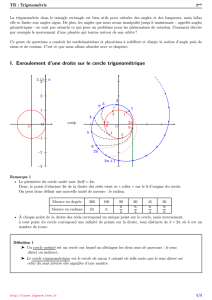
3- Enroulement de la droite des réels sur le cercle trigonométrique
Soient ( O;I;J) un repère orthonormé, C le cercle trigonométrique de centre O et D la droite des réels
tangente à C en I.
En enroulant la droite D autour du cercle trigonométrique C , on peut associer à chaque réel (repéré sur
D ) un unique point M de C , qu’on note M(x) et qu’on appelle point associé au réel x.
Remarques :
• si x☻[O;π] alors x désigne la longueur de l’arc È IM .
• Si x☻[-π;0] alors –x=
| |
x désigne la longueur de l’arc È IM .
Exemple :
Placer sur le cercle trigonométrique ci-contre, les points
associés aux réels suivant :
O ; π ; -
π
2
;
π
2
;
π
4
; -
3π
4
; 2π ; -π ;
7π
2
.
II. Cosinus et sinus d’un nombre réel
1- Définition
Soit (O;I;J) un repère orthonormé, C le cercle trigonométrique de centre O, x un réel et
M(x) le point de C associé au réel x.
On appelle cosinus de x et on note cos(x) l’abscisse du point M dans le repère ( O;I;J).
On appelle sinus de x et on note sin(x) l’ordonnée du point M dans le repère ( O;I;J).
M
I
O
O I
J
M(x)
cos(x)
sin(x)
O
I
J

_________________________________________________________________________________________________
Cours S1 : Trigonométrie Page 2 sur 4
2- lien entre la trigonométrie du triangle rectangle
Cette définition du cosinus et du sinus est cohérente avec celle connue du triangle rectangle.
En effet, soit x un réel de l’intervalle 0;
π
2
et M son point associé sur C .
x désigne donc la longueur de l’arc È IM . On note H le projeté orthogonal de M sur l’axe des
abscisses, le triangle OHM est donc rectangle en H et on a :
On a donc OH=cos(x), HM=sin(x) et OM=1.
D’où cos
( )
Æ
HOM =
côté adjacent
hypoténuse
=
OH
OM
=
cos(x)
1
=cos(x)
Et sin
( )
Æ
HOM =
côté opposé
hypoténuse
=
HM
OM
=
sin(x)
1
=sin(x)
3- Les valeurs remarquables à connaître
x 0
π
6
π
4
π
3
π
2
π
cos(x)
sin(x)
4- Propriétés du cosinus et du sinus d’un réel x
• Quel que soit le réel x
• cos
2
(x)+sin
2
(x)=1
• -1Âcos(x)Â1
• -1Âsin(x)Â1
• cos(-x)=cos( x) et sin(-x)=sin(x)
• cos(x+2π)=cos(x) et sin( x+2π)=sin(x)
Démonstrations : La première propriété sera montrer en exercice
• A chaque réel x, on associe un point M(x) du cercle C de centre O et de rayon 1 donc l’abscisse et l’ordonnée du point M
sont évidemment des réels de l’intervalle [-1;1].
• Puisque
| |
x=
| |
-x les points M(x) et M(-x) sont symétriques par rapport à l’axe des abscisses, ils ont donc même abscisse et
des ordonnées opposées donc cos(-x)=cos(x) et sin(-x)=sin(x)
• La longueur de C est 2π donc les points M(x) et M(x+2π) sont confondus, ils ont donc même abscisse et même ordonnée
d’où cos(x+2π)=cos(x) et sin(x+2π)=sin(x).
III. Les fonctions (de référence) trigonométriques : x→cos(x) et x→sin(x)
1- Fonction cosinus
a. Définition :
On appelle fonction cosinus la fonction, notée cos, définie sur IR, qui à tout réel x associe le réel cos(x).
cos : IR ↔ IR
x → cos(x)
b. Parité :
La fonction cosinus est définie sur IR (ensemble centré en zéro).
De plus, nous avons vu que : ┐ x☻IR, cos(-x)=cos( x).
On en déduit donc que la fonction cosinus est paire.
Sa courbe représentative est donc symétrique par rapport à l’axe des ordonnées.
c. Périodicité :
Nous avons vu que : ┐x☻IR, cos(x+2π) = cos(x).
La courbe représentative de la fonction cosinus va donc se reproduire périodiquement sur une période de 2π.
On dit que la fonction cosinus est périodique de période 2π.
d. Ensemble d’étude de la fonction cosinus :
O
I
J
M(x)
O
I
J
H

_________________________________________________________________________________________________
Cours S1 : Trigonométrie Page 3 sur 4
La fonction cosinus est périodique de période 2π, on peut donc se contenter de l’étudier sur un intervalle de longueur 2π, par exemple
[-π;π].
De plus la fonction cosinus est paire, on peut donc se contenter de l’étudier sur [0;π].
e. Sens de variation sur [0;π] :
On utilise le cercle trigonométrique :
f. Courbe représentative :
• On trace la courbe sur [0;π] en utilisant quelques valeurs.
• La fonction est paire, la courbe est donc symétrique par rapport à l’axe des
ordonnées. On obtient donc le tracé de la courbe sur [-π;π] càd sur une
période.
• On utilise la périodicité : on reproduit la courbe de façon périodique.
2- Fonction sinus
a. Définition :
On appelle fonction sinus la fonction, notée sin, définie sur IR, qui à tout réel x associe le réel sin(x).
sin : IR ↔ IR
x → sin(x)
b. Parité :
La fonction sinus est définie sur IR (ensemble centré en zéro).
De plus, nous avons vu que : ┐ x☻IR, sin(-x)=-sin(x).
On en déduit donc que la fonction sinus est impaire.
Sa courbe représentative est donc symétrique par rapport à l’origine du repère.
c. Périodicité :
Nous avons vu que : ┐x☻IR, sin(x+2π) = sin(x).
La courbe représentative de la fonction sinus va donc se reproduire périodiquement sur une période de 2π.
On dit que la fonction sinus est périodique de période 2π.
d. Ensemble d’étude de la fonction cosinus :
La fonction sinus est périodique de période 2π, on peut donc se contenter de l’étudier sur un intervalle de longueur 2π, par exemple
[-π;π].
De plus la fonction sinus est impaire, on peut donc se contenter de l’étudier sur [0;π].
e. Sens de variation sur [0;π] :
On utilise le cercle trigonométrique :
x 0 π
3 π 2 π
cos(x)
J
I
O
J
I
O
1
0
π

_________________________________________________________________________________________________
Cours S1 : Trigonométrie Page 4 sur 4
f. Courbe représentative :
a. On trace la courbe sur [0;π] en utilisant quelques valeurs.
b. La fonction est impaire, la courbe est donc symétrique par
rapport à l’origine. On obtient donc le tracé de la courbe sur
[-π;π] càd sur une période.
c. On utilise la périodicité : on reproduit la courbe de façon
périodique.
IV. Exercices
Exercice 1
On considère un repère orthonormé ( O;I;J) d’unité graphique 4cm.
1- Tracer dans ce repère, le cercle trigonométrique de centre O.
2- Placer le point M associé au réel
π
4
. Déterminer un réel positif et un réel négatif tels que leurs points associés soient
confondus avec M.
3- Déterminer la valeur exacte de sin
25π
4
et cos
25π
4
.
4- Même question avec sin
15π
4
et cos
15π
4
.
Exercice 2
L’objectif de cet exercice est de montrer que pour tout réel x, cos
2
(x)+sin
2
(x)=1
On considère dans un repère (O;I;J) orthonormé le cercle trigonométrique de centre O et on considère un réel x. soit M le point de
C associé à x.
1- 1
er
cas : l’abscisse de M est un réel positif.
a. Placer un point M
1
correspondant à cette situation.
b. On appelle H et K les projetés orthogonaux de M
1
sur les axes.
En considérant le triangle OM
1
H, montrer que cos
2
(x)+sin
2
(x)=1.
2- 2
ème
cas : l’abscisse de M est un réel négatif.
a. Placer un point M
2
correspondant à cette situation.
b. On appelle P et q les projetés orthogonaux de M
é
sur les axes.
En considérant le triangle OPM
2
, montrer que cos
2
(x)+sin
2
(x)=1.
Exercice 3
On considère les fonctions f et g sur Ë par f(x)=cos
( )
-3x
2
et g(x)=sin -3x
2
+
3π
2
.
1- Donner le procédé de calcul permettant de passer de x à f(x) puis celui permettant de passer de x à g(x).
2- Déterminer les variations de f et de g sur 0;
π
3
.
x 0 π
6 π 2 π
sin(x)
1
0
π