TD1-Generalites sur les fonctions-1S2

LYCEE M.T.B.M DE DAROU MOUSTY ANNEE SCOLAIRE : 2008 – 2009
CLASSE DE 1re S2 DISCIPLINE : MATHEMATIQUES
Généralités sur les fonctions
Exercice 1
1. Construire dans des repères différents la représentation graphique des fonctions de référence :
2
xx 
;
3
xx 
;
x
x1
;
xx 
2. En déduire les représentations des fonctions suivantes :
a)
2
2
1
:+
−x
xf 
b)
2)1(: 3−−xxg 
c)
12: −+xxh 
d)
2
)2(: +xxi 
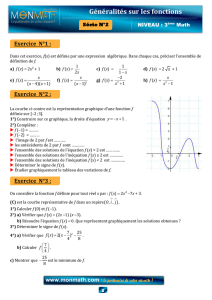
Exercice 2
Le plan est muni d’un repère orthogonal. Soit f la fonction de R vers R, définie par
24)( 2++= xxxf
et (C) sa représentation graphique.
1. a) Déterminer les nombres réels a, b et c tels que, pour tout nombre réel x, on a :
baxxf ++= 2 )()(
.
b) Construire (C).
2. Résoudre graphiquement :
a) l’équation
224
2=++ xx
b) l’inéquation
224
2>++ xx
Exercice 3
1. Soit u et v les fonctions définies respectivement par :
xx)x(u 2+=
et
2x
x
)x(v − =
a) On pose
uvf =
. Déterminer
f
D
le domaine de définition de f.
b) Donner l’expression de f(x).
2. Soit g la fonction définie par :
x6x3
10x13x3
)x(g 2
2
+
++
=
.
Résoudre dans
] [
∞+;2
, l’inéquation
1)x(g ≤
3. a) Démontrer que, pour tout réel x :
)5xx6)(2x(10x3x13x6 223 −++=−−+
.
b) Résoudre dans IR l’équation (f + g) (x) = 0.
Exercice 4
Soit f la fonction numérique à variable réelle définie par :
3x6x
x42x
)x(f 2+−
−−−
=
.
1. Déterminer l’ensemble de définition de f.
2. Montrer que le point Ω (3 ; 0) est centre de symétrie de la courbe de f.
Exercice 5
1. Soit f et g définies sur IR par :
xx4x3)x(f 23 −+−=
et
1x2
3x
)x(g
2
−
−
=
.
Déterminer les domaines de définition de f et de g.
2. h et k sont deux fonctions définies sur IR par :
3x5
x3x
)x(h
3
−
+−
=
et
)x1)(x1(
x2
)x(k
4
+−
+
=
Etudier les parités des fonctions h et k.

Exercice 1 :
Etudier la parité des fonctions f et g définies par :
a)
( )
42
2
5
4
xx
fx x
+−
=−
; b)
( )
1
x
gx
x
=
+
Exercice 2 :
Soit la fonction f telle que
( )
231
2
xx
fx x
++
=+
.
1) Déterminer une équation de
( )
f
C
dans le repère
( )
;,ijΩ
rr
,
( )
2; 1Ω− −
2) Que peut-on en déduire pour
( )
f
C
.
Exercice 3 :
Soit l’application
[ [
:2,fIR
+
+∞ →
2xx−a
.
1) Démontrer que f est une bijection. Déterminer
1
f−
.
2) Construire la courbe de
1
f−
dans un repère orthonormal. En déduire celle de f.
GENERALITES SUR LES FONCTIONS NUMERIQUES D’UNE VARIABLE REELLE
Exercice 1 :
Le plan est muni d’un repère orthogonal
( )
;,OI J
.
( )
C
est la courbe représentative d’une fonction f, d’ensemble
de définition
39
22
;−
"#
$%
&'
.
1) Construire la courbe représentative
( )
g
C
de la fonction
3
2
:2gx f x
!"
+−
$%
&'
a
.
2) a) Construire la courbe représentative
( )
h
C
de
( )
:hx f x−a
.
b) Déduire de
( )
C
et de
( )
h
C
la représentation graphique de la fonction
( )
xfxa
Exercice 2 :
( )
C
est la courbe représentative dans le plan muni
d’un repère
( )
;,OI J
d’une fonction f dont l’ensemble de
définition est :
[ [ ] ]
4; 2 2; 3−−∪−
Tracer la courbe représentative et déterminer l’ensemble de
définition de chacune des fonctions suivantes : a)
( )
xfx−a
;
b)
( )
xfxa
; c)
( )
2xfx+a
; d)
( )
23xfx−−a
Exercice 3 :
On donne la courbe
( )
C
représentative de la fonction
3
:
4
x
fx −a
, la courbe
( )
1
C
translatée de
( )
C
par la translation
de vecteur
132Uij=+
rr
et la courbe
( )
2
C
translatée de
( )
C
par la
translation de vecteur
242Uij=− −
rr
.
( )
1
C
et
( )
2
C
sont les courbes représentatives des fonctions
1
f
et
2
f
.
Etablir une expression de
( )
1
fx
et de
( )
2
fx
en fonction de x.
Exercice 4 :
On donne la courbe
( )
C
représentative de la fonction

32
:32fx x x−+a
. Reproduire la courbe
( )
C
, puis en déduire, sur le
même graphique, les courbes
( )
1
C
et
( )
2
C
représentatives des fonctions
1
f
et
2
f
définies par :
( )
32
132fx x x=−+
et
( )
32
232fx x x=−+
.
Exercice 5 :
Soit f la fonction définie par :
( )
221fx x x=−+
.
1) Montrer que la droite
( )
:3Dx=−
est axe de symétrie de
f
C
.
2) Ecrire
( )
fx
sous la forme canonique.
3) Soit
( )
1, 3A−
dans le repère
( )
;,Oi j
rr
. En utilisant un changement de repère par la
translation de vecteur
OA
uuur
, donner l’équation cartésienne de
f
C
dans le repère
( )
;,Ai j
rr
.
4) Représenter graphiquement f.
5) En déduire la représentation graphique de la fonction g définie par :
( ) ( )
gx f x=
.
Exercice 6 :
Soit f la fonction définie par :
( )
41
5
x
fx x
−
=−
.
1) Déterminer deux réels a et b tels que
( )
5
b
fx a x =+−
.
2) Soit
f
C
la courbe représentative de f dans le repère
( )
;,Oi j
rr
. Donner une équation de
f
C
dans le repère
( )
;,ijΩ
rr
où
( )
5, 4Ω
.
3) Représenter
f
C
dans le repère
( )
;,ijΩ
rr
.
4) Résoudre graphiquement l’inéquation
41
0
5
x
x
−≤
−
.Retrouver les résultats
algébriquement.
5) En déduire la représentation graphique de la fonction g définie par :
( )
41
5
x
gx x
−
=−
.
Exercice 7 :
Soit h la fonction définie sur l’intervalle
[ [
1, 4I=
par :
( )
1hx x=−
.
1) Montrer que h réalise une bijection de I vers un intervalle J à préciser.
2) Représenter graphiquement
h
C
dans un R.O.N
( )
;,Oi j
rr
. En déduire la représentation
1
h
C−
de la
bijection réciproque de h.