MECA.Solide-Torseur2021 22

MECANIQUE DES SOLIDES INDEFORMABLES
Professeur K. Bouabid
Filière SMP3, Année 2021/22
Sommaire:
I. Les torseurs
II. Géométrie des masses
III. Cinématique du solide
IV. Cinétique du solide
V. Théorèmes généraux Galilée:1564 -1642
Issac Newton:1642 -1726

Chapitre I : Les Torseurs
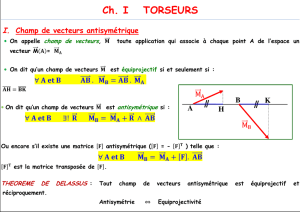
Un torseur est un outil mathématique qui permet de modéliser et de représenter un champ de vecteurs
équiprojectifs : champ des vitesses, champ des moments, champs des moments cinétique, champ des moments
dynamique…
Les prérequis:
-Produit scalaire
-Produit vectoriel
-Produit mixte
▪Les espaces vectoriel () et affine (considérés dans ce cours sont des espaces de dimension 3 (sauf mention
contraire)
▪E est représenté dans un repère orthonormé direct R d’origine O de base : R(O,)
Autrement, c’est un outil mathématique utilisé en mécanique du solide indéformable, pour décrire les
mouvements des solides et les actions mécaniques qu’ils subissent de la part d’un environnement extérieur.

I. Applications antisymétriques
I.1 Définition
une application de E dans E
Eest associé à un espace affine qui a chaque point M de associe le vecteur appelé
champ des vecteurs.
(Exemples : Champ des vitesses, champ des accélérations, champ de forces, champ électrique,
champ magnétique,…etc.)
est aussi une application linéaire : , 
est antisymétrique si et , on a : 

I.2 Expression analytique d’une fonction linéaire antisymétrique
La représentation analytique de l’application f est une matrice Ldonnée
par :   
est antisymétrique  
donc 
Donc : 
De même :
Donc :  
La matrice d’une application antisymétrique(symétrique) est antisymétrique(symétrique)

Avec est par définition le vecteur de l’application antisymétrique .
On montre que est unique .
On peut déterminer par la relation :  