Calcul d`aire par exhaustion

Visualisation de la méthode par
exhaustion pour calculer l’aire
sous une courbe
Bien comprendre le principe d’aire par
exhaustion en utilisant une série d’aires de
rectangles

2
Introduction
Intégrer aura pour nous deux sens :
Dans un premier temps, intégrer voudra dire: « calculer le tout
de ou donner la somme ou le total de ». Par exemple,
rechercher le déplacement total lorsque nous connaissons la
fonction vitesse. Ce sens donné au mot intégrer fait référence à
l’intégrale définie et est lié au calcul d’aire sous la courbe.
Ensuite, intégrer signifiera « trouver une fonction dont la
différentielle est connue ». Par exemple, lorsque nous
connaissons la fonction vitesse, nous pouvons trouver la
fonction position.

3
Mouvement et calcul d’aire
Cas d’une vitesse constante
Le déplacement d’un mobile dans un certain intervalle de temps
est donnée par :
déplacement = vitesse × Δ temps
Dans le cas où la vitesse est positive, le déplacement correspond
à la distance parcourue.
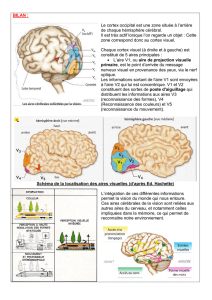
Dans le cas d’une
vitesse constante,
le déplacement
correspond à l’aire
du rectangle. Que
se passe-t-il dans le
cas d’une vitesse
variable.
vitesse (m/min)
temps (min)
Vitesse en fonction du temps
vitesse × Δ temps =
déplacement

4
Dans le cas d’une vitesse
variable, Comment peut-on
calculer le déplacement?
Mouvement et calcul d’aire
Cas d’une vitesse variable
Vitesse en fonction du temps
0
100
200
300
400
500
600
0 2 4 6 8 10
temps t (min)
vitesse v (m/min)
Temps t (min) Vitesse (m/min)
0350
2400
4450
6550
8400
10 375
Vitesse au temps t
Comment trouver une approximation
du déplacement si nous possédons
l’information suivante sur la vitesse:

5
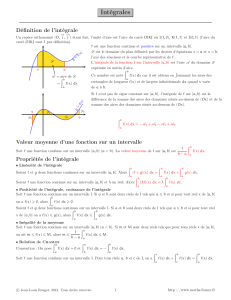
Dans le cas d’une vitesse variable,
nous pouvons approximer le
déplacement par la somme des aires de
rectangles.
Calcul du déplacement à l’aide du calcul des
aires de rectangles
Nous découpons alors notre intervalle de
temps en petits sous intervalles de temps
et sur chacun d’eux nous assumons que la
vitesse est constante.
Dans l’exemple illustré ci-contre, nous avons découpé l’intervalle en 5 sous
intervalles de 2 minutes et, pour chaque sous intervalle, nous assumons
que le mobile roule à une vitesse constante.
Pour chaque sous intervalle de temps, l’aire du rectangle nous donne alors une
approximation du déplacement du mobile dans ce sous intervalle.
Le déplacement total est la somme de ces petits déplacemnents.
Comment évaluerons-nous le déplacement total?
700
m
800
m
900
m
1100
m
800
m