Oraux-2015-solutions

A=
1a a2a3
1/a 1a a2
1/a21/a 1a
1/a31/a21/a 1
A
A
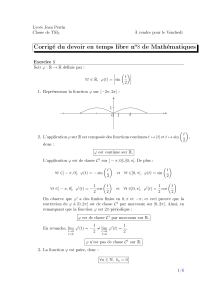
f∈ C(R,R)
∀x∈R, f(x) + x
0
(x−t)f(t)dt = 1
C1, C2, C3, C4A
C2=aC1, C3=a2C1, C4=a3C1
A
4−3 = 1 x+ay +a2z+a3t= 0
λ1=λ2=λ3= 0 λ4(A)=4 λ4= 4
(A)C1
A
•f∈ C(R,R)∀x∈R, f(x) + x
0
(x−t)f(t)dt = 1
∀x∈R, f(x)=1−xx
0
f(t)dt +x
0
tf(t)dt
t7→ f(t)t7→ tf(t)x7→ x
0f(t)dt x 7→ x 0tf(t)dt
C1RfC1
∀x∈R, f′(x) = −xf(x)−x
0
f(t)dt +xf(x)
∀x∈R, f′(x) = −x
0
f(t)dt
f′C1fC2
∀x∈R, f′′(x) = −f(x)
fRy′′ +y= 0
A B ∀x∈R, f(x) = Acos x+Bsin x
∀x∈R, A cos x+Bsin x+x
0
(x−t)(Acos t+Bsin t)dt = 1
⇒ ∀x∈R, A cos x+Bsin x+xx
0
(Acos t+Bsin t)dt −x
0
t(Acos t+Bsin t)dt = 1

∀x∈R, A cos x+Bsin x+x(Asin x−Bcos x+B)−[t(Asin t−Bcos t)]x
0+x
0
(Asin t−Bcos t)dt = 1
⇒ ∀x∈R, A cos x+Bsin x+Ax sin x−Bx cos x+Bx −(Ax sin x−Bx cos x)+[−Acos t+Bsin t]x
0= 1
⇒ ∀x∈R, A cos x+Bsin x+Bx + (−Acos x+A−Bsin x) = 1
⇒ ∀x∈R, Bx +A= 1
x A = 1 B= 0
∀x∈R, f(x) = cos(x)
A= 1 B= 0
f= cos
f
C2
A=
3−3 2
−1 5 −2
−1 3 0 
M3(R)
R R2=A R
RM3(R)A=R2
f:R−→ R
∀(x, y)∈R2, f x+y
2=1 2(f(x) + f(y)) R
fRf(0) = f(1) = 0
f
f f
f(2x) = 2f(x)
f
fR
A=
3−3 2
−1 5 −2
−1 3 0 
χA(x) = 
3−x−3 2
−1 5 −x−2
−1 3 −x
=
2−x−3 2
2−x5−x−2
2−x3−x
χA(x) = (2 −x)
1−3 2
1 5 −x−2
1 3 −x
= (2 −x)
1−3 2
0 8 −x−4
0 6 −2−x
= (2 −x)[(x−8)(x+ 2) + 24]
χA(x) = (2 −x)(x2−6x+ 8) = (2 −x)(x−2)(x−4)
χA(X) = −(X−2)2(X−4)
E4(A)
dim(E2(A)) = 3 −(A−2I3)
A−2I3=
1−3 2
−1 3 −2
−1 3 −2
dim(E2(A)) = 3 −1 = 2 = (2)
χA(X) = −(X−2)2(X−4) R[X]
AM3(R)
P∈GL3(R)A=P. 
200
020
004
.P −1
R=P. 
√2 0 0
0√2 0
0 0 2 
.P −1R2=P. 
200
020
004
.P −1=A
A Q(X) = 
λ∈Sp(A)
(X−λ) = (X−2)(X−4)
A

R∈M3(R)R2=A
Q(A) = (A−2I3)(A−4I3)=0=(R2−2I3)(R2−4I3)
T(X) = (X2−2)(X2−4) = (X−√2)(X+√2)(X−2)(X+ 2)
RR[X]R
fRR
∀(x, y)∈R2, f x+y
2=1 2(f(x) + f(y)) f(0) = f(1) = 0
x y =−x
∀x∈R, f x−x
2=f(0) = 0 = 1 2(f(x) + f(−x))
∀x∈R, f(−x) = −f(x)f
x y = 2 + x
∀x∈R, f(x+ 2) −f(x) = f(x+ 2) + f(−x) = 2f(x+2)+(−x)
2= 2f(1) = 0
∀x∈R, f(x+ 2) = f(x)f
•f[0,2]
M∈R+,∀x∈R,|f(x)|6M
f∀x∈R,|f(x)|6M f
x y = 0
∀x∈R, f x+ 0
2=1 2(f(x) + f(0)
=0
)∀x∈R, f(x) = 2fx
2
x∀x∈R, f(2x) = 2f(x)
∀x∈R, f(4x) = 2f(2x) = 4f(x)
∀x∈R,∀k∈N, f(2kx) = 2kf(x)
f x0∈Rf(x0)̸= 0 ∀k∈N, f(2kx0)=2kf(x0)−→
k→+∞±∞
f x0f(x0)
f
fRR
∀(x, y)∈R2, f x+y
2=1 2(f(x) + f(y))
f(0) = f(1) = 0
x7→ ax +bR
∀x∈R, g(x) = f(x)−(ax +b)gR
a b g g(0) = g(1) = 0
g(0) = 0 ⇐⇒ f(0) −b= 0 ⇐⇒ b=f(0)
g(1) = 0 ⇐⇒ f(1) −a−b= 0 ⇐⇒ a=f(1) −b=f(1) −f(0)
g:x7→ f(x)−(f(1) −f(0))
a
x−f(0)
b
R
g(0) = g(1) = 0
∀x∈R, f(x) = ax +b f
R
an=+∞
0
sin t
n
t(1 + t2)dt
(an)
uMn(R)
∀M∈Mn(R), u(M) = 1
3(2M−tM)
u u
(u) det(u)
•n∈N∗t7→ sin t
n
t(1 + t2)]0,+∞[
sin t
n
t(1 + t2)∼
t→0
t
n
t(1 + t2)=1 n
1
1 + t2∼
t→0
1
nlim
n→+∞
sin t
n
t(1 + t2)=1 n

t7→ sin t
n
t(1 + t2)[0,+∞[
1
n[0, a], a > 0
∀u∈R,|sin u|6|u| ∀n∈N∗,∀t∈R,
sin t
n
t(1 + t2)
6t/n
t(1 + t2)=1 n(1 + t2)
n∈N∗t7→ 1
n(1+t2)]0,+∞[ [0,+∞[
t7→ sin t
n
t(1 + t2)]0,+∞[
ann∈N∗
•
∀n∈N∗,|an|=+∞
0
sin t
n
t(1 + t2)dt
6+∞
0
sin t
n
t(1 + t2)
dt 6+∞
0
dt
n(1 + t2)=π 2×1 n
lim
n→+∞an= 0
• ∀n∈N∗, an=+∞
0
sin t
n
t(1 + t2)dt =1 n+∞
0
sin t
n
t
n×1
1 + t2dt
∀n∈N∗,∀t∈]0,+∞[, gn(t) = sin t
n
t
n×1
1 + t2
lim
u→0
sin u
u= 1 ∀t∈]0,+∞[,lim
n→+∞gn(t) = 1
1 + t2
|sin u|6|u|
∀n∈N∗,∀t∈]0,+∞[,|gn(t)|61
1+t2t7→ 1 1+t2]0,+∞[
[0,+∞[
lim
n→+∞+∞
0
gn(t)dt =+∞
0
1
1 + t2dt = [ t]+∞
0=π
2
an=1
n+∞
0
sin t
n
t
n×1
1 + t2dt =1 n+∞
0
gn(t)dt
an∼
t→0
π
2n
•λ∈RM∈Mn(R)− {0}
u(M) = λ.M ⇐⇒ 2M−tM= 3λM
⇐⇒ −tM= (3λ−2)M
⇐⇒ M= (2 −3λ)tM
=⇒M= (2 −3λ)(2 −3λ)M
=⇒(2 −3λ)2= 1 M̸= 0
=⇒2−3λ= 1 2 −3λ=−1
=⇒λ= 1 λ=1
3(u)⊂1,1 3
• ∀M∈Mn(R), u(M) = M⇐⇒ 2M−tM= 3M⇐⇒ tM=−M
u
Mn(R)E1(u) = An(R)n(n−1)
2
• ∀M∈Mn(R), u(M) = 1
3M⇐⇒ 2M−tM=M⇐⇒ tM=M
1
3u
Mn(R)E1
3(u) = Sn(R)n(n+1)
2
•Sn(R)An(R)Mn(R)
uMn(R)u
•Mn(R)Sn(R)An(R)u
n(n−1)
2= dim(E1(u)) n(n+1) 2= dim(E1
3(u)) 1
3
(u) = n(n−1)
2+1 3
n(n+ 1)
2=3n2−3n+n2+n 6=n2−n 3
det(u) = 1n(n−1)
2×1
3n(n+1)
2
=1
3n(n+1)
2

a∈R
f:t7→ 1
t+a
fR+R+ f(t)dt
u=et
A∈ Mn(R) 2A3+ 3A2+ 6A−In= 0
A
AMn(C)
det(A)>0
D={(x, y)∈R2, x2+y261}f
∀(x, y)∈ D, f(x, y) = x3−3x(1 + y2)
fD
t7→ t+aR+∀x∈R, x >1
f:t7→ 1
t+aR+
[0, b]
f(t) = 1
t+a=2 et+e−t+ea+e−a62 et= 2e−t
t7→ 2e−tR+f
•J=+∞
0
dt
t+a=+∞
0
2etdt
e2t+ 2 a et+ 1
u=etJ=+∞
0
2du
u2+ 2u a + 1
J=+∞
0
2du
(u+a)2−2a+ 1 =+∞
0
2du
(u+a)2−2a=+∞
0
2du
(u+a+a)(u+a−a)
=+∞
0
2du
(u+ea)(u+e−a)
2
(u+ea)(u+e−a)=(u+ea)−(u+e−a) (u+ea)(u+e−a)×2 ea−e−a=1 a1 u+e−a−1 u+ea
+∞
0
1
u+e±adu J
x
0
1
u+e±adu
x > 0, Jx=x
0
dt
t+a=1 ax
0
1
u+e−adu −x
0
1
u+eadu
Jx=1
aln u+e−a u+eax
0
=1
aln x+e−a x+ea−ln e−2a
x→+∞,x+e−a
x+ea→1 ln x+e−a x+ea→0
J= lim
x→+∞Jx=−ln(e−2a)
a=2a a
A∈ Mn(R) 2A3+ 3A2+ 6A−In= 0
A(2A2+ 3A+ 6In) = InA A−1= 2A2+ 3A+ 6In
P(X) = 2X3+ 3X2+ 6X−1A
n P
∀x∈R, P ′(x) = 6x2+ 6x+ 6 = 6(x2+x+ 1) >0
PR−∞ +∞
α P (0) = −1P α > 0
P(X)
P(X)β β
α, β β P (X)
P(X)C[X]
AMn(C)
C(A)⊂ {α, β, β}
AMn(C)