Fonction dérivée

DÉRIVÉE ET VARIATIONS D'UNE
FONCTION
1re PRO
1/3
Objectifs
Connaissances (A SAVOIR)
Capacités (A SAVOIR FAIRE)
 Sécantes à une courbe passant par un point.
 Tangente à une courbe en un point.
 Nombre dérivé.
 Équation réduite de la tangente à une courbe en
un point.
 Fonction dérivée d’une fonction dérivable sur un
intervalle. Notation f ’.
 Fonctions dérivées des fonctions affines et carré.
 Règles de dérivation : dérivée du produit d’une
fonction dérivable par une constante, dérivée de la
somme de deux fonctions dérivables.
 Lien entre signe de la dérivée d’une fonction sur
un intervalle et sens de variation de cette fonction
sur cet intervalle.
 Extremum d’une fonction sur un intervalle donné.
Extremum local et extremum global.
 Fonction polynôme de degré inférieur ou égal à 2.
 Fonction inverse.
 Construire en un point la tangente à la courbe
représentative d’une fonction f à l’aide d’outils
numériques.
 Déterminer, par une lecture graphique, lorsqu’il
existe, le nombre dérivé d’une fonction f en
l’abscisse d’un point de la courbe représentative
de cette fonction.
 Construire en un point la tangente à la courbe
représentative d’une fonction f connaissant le
nombre dérivé en ce point.
 Écrire l’équation réduite de la tangente à une
courbe en un point lorsqu’elle existe.
 Utiliser les formules et les règles de dérivation
pour déterminer la dérivée d’une fonction
polynôme de degré inférieur ou égal à 2.
 Étudier, sur un intervalle donné, les variations
d’une fonction à partir du calcul et de l’étude du
signe de sa dérivée. Dresser son tableau de
variations.
 Déterminer un extremum d’une fonction sur un
intervalle donné à partir de son sens de variation.
 Dresser le tableau de variations d’une fonction
polynôme de degré inférieur ou égal à 2.
 Étudier la fonction inverse : dérivée, variations,
représentation graphique. Dresser son tableau de
variations.
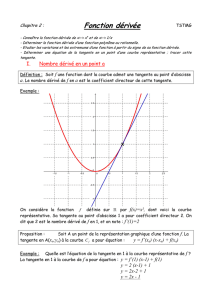
1. Tangente à une courbe en un point
1.1. Tangente et nombre dérivé
La droite qui approche au mieux la courbe représentative d’une fonction au voisinage d’un
point A est appelée tangente à la courbe au point A (elle coupe la courbe qu’en un seul point).
Soit f une fonction dont la
courbe représentative admet
une tangente au point A
d’abscisse xA.
Le coefficient directeur de la
tangente à la courbe
représentative de la fonction f
au point de coordonnées (xA ;
f(xA)) est appelé nombre
dérivé de f en xA.
Le nombre dérivé de f en xA
est noté f ’(xA).
x
1
2
xA = 3
4
0
10
20
30
40
50
60
y
f
T
A
1
+15
f(x) = x3 – 2x2 + 30
Nombre dérivé
=
Coefficient
directeur de la
tangente
f ’(3) = 15

DÉRIVÉE ET VARIATIONS D'UNE FONCTION
1re PRO
2/3
1.2. Équation d’une tangente
Soit f une fonction dont la courbe représentative admet une tangente au point A d’abscisse xA.
L’équation réduite de cette tangente est y = f ’(xA)×(x – xA) + f(xA)
2. Fonction dérivée
2.1. Définition
Soit f une fonction définie sur un intervalle I et admettant, pour tout x de l’intervalle I, un
nombre dérivée f ’(x).
La fonction qui, à tout x de l’intervalle I associe le nombre dérivé f ’(x) de f est appelée
fonction dérivée de f : elle est notée f ’.
2.2. Fonctions dérivées des fonctions élémentaires
Soit f une fonction définie sur un intervalle I, et a et b deux nombres réels donnés :
Fonction f
Dérivée f ’
Ensemble de définition I :
f(x) = a
f ’(x) = 0
f(x) = ax + b
f ’(x) = a
f(x) = x2
f ’(x) = 2x
Soient f et g deux fonctions admettant sur
l’intervalle I des dérivées f ’(x) et g’(x).
Soit a un nombre réel donné.
Dans ces conditions, pour tout x de I on a :
Fonction
Dérivée
a.f(x)
a.f ’(x)
f(x) + g(x)
f ’(x) + g’(x)
3. Études de fonction à l’aide de la dérivée
3.1. Sens de variation
Soit f une fonction définie sur un intervalle [a ; b] et admettant sur cet intervalle une dérivée f ’
•Si pour tout x de [a ; b] on a f ’(x) > 0,
alors la fonction f est croissante sur [a ; b].
x
a b
f ’(x)
+
f
•Si pour tout x de [a ; b] on a f ’(x) < 0,
alors la fonction f est décroissante sur [a ; b].
x
a b
f ’(x)
–
f
•Si pour tout x de [a ; b] on a f ’(x) = 0, alors la fonction f est constante sur [a ; b].
3.2. Extremums
Si la dérivée s’annule en changeant de signe en un point x0, alors la fonction admet un
extremum en x0. Un extremum est un minimum ou un maximum.
x
a x0 b
f ’(x)
–0+
f
f(x0)
la fonction f possède pour x0 un minimum
égal à f(x0)
x
a x0 b
f ’(x)
–0+
f
f(x0)
la fonction f possède pour x0 un maximum
égal à f(x0)

DÉRIVÉE ET VARIATIONS D'UNE FONCTION
1re PRO
3/3
4. Fonction inverse
Soit la fonction f qui à tout x non nul associe le nombre 1
x.
Cette fonction est définie par f(x) = 1
x (pour x  0).
Sa fonction dérivée est f ’(x) = – 1
x2 (pour x  0).
Pour tout x  0, on a x2 > 0 donc – 1
x2 < 0 soit f ’(x) < 0 et on peut alors en déduire le tableau de
variation de la fonction f suivant :
x
–0 +
f ’(x)
–
–
f
La double barre sous le zéro indique que la
fonction n’est pas définie en x = 0.
La courbe représentative de la fonction inverse
est appelée hyperbole.
-4
-2
2
4
-8
-6
-4
-2
0
2
4
6
8
y
x
f(x) = 1
x