MATHEMATIQUE 1 Calcul différentiel et intégral Enseignant : AKOWANOU Christian Djidjoho Maitre de Conférences des Universités (CAMES) Enseignant Chercheur 1 Objectif : Maîtriser les notions du calcul différentiel et intégral utilisées dans les autres cours de mathématiques et dans les cours de génie. Contenu : Analyse : Généralités sur les fonctions de : fonctions exponentielles, fonctions logarithmiques, fonctions trigonométriques, fonctions trigonométriques inverses. Calcul différentiel : Limites, dérivées des fonctions élémentaires, règles de dérivations, étude de graphes, etc. Calcul intégral : Intégrales indéfinies, méthodes d’intégration, utilisation des tables, intégrales définies, application au calcul d’aires, de longueurs d’arcs, de volumes, intégrales impropres, … Suites et séries : Développements limités (Taylor, Marc Laurin) - suites et séries évaluation de fonctions et d’intégrales définies à l’aide de série. Séances de TD : Composés d’exercices choisis pour illustrer et compléter la théorie vue au cours. 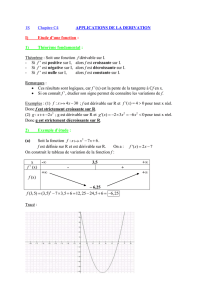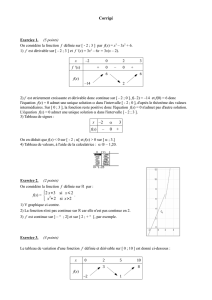2 Chapitre 1 Généralités sur les fonctions d’une variable réelle 1-Définitions et théorèmes essentiels Définition 1 Soient notée et deux sous-ensembles de telle que, à tout . On appelle fonction, toute relation de , on associe au plus une image L’ensemble A est dit ensemble de départ de appelé antécédent et et vers . son ensemble d’arrivée. est une image. Exemple Considérons la relation Trouvons l’image par : des éléments : , 0, 2, 5 1/2 0 2 5 Pas d’image Pas d’image 1 Cette relation est une fonction puisque les conditions de la définition de fonction sont requises. Définition 2 Considérons la fonction : On appelle domaine de définition de que l’on note par exemple l’ensemble définit par Exemple Considérons la fonction : Indiquer le domaine de définition de 3 Définition 3 Considérons la fonction : On dira que est une application si son domaine de définition (noté D) est confondu à son ensemble de départ, soit . Exemple Considérons la fonction Montrer que : est une application Solution l’ensemble de départ, déterminons le domaine de définition En effet, ici Posons alors Nous constatons donc que de . et . Ainsi est une application. Définition 4 Considérons la fonction définie sur un sous-ensemble définition de . On dira que est croissante sur , si c’est-à-dire est le domaine de , on a Fig : Allure de la courbe d’une fonction croissante Définition 5 Soit la fonction définie sur un intervalle , . On dit que est décroissante sur , si on a 4 Fig : Allure d’une courbe de fonction décroissante Remarque De la définition 4, si on a croissante sur . De la définition 5, si on a strictement décroissante sur . . On dit que f est strictement . On dit alors que f est Définition 6 Si la fonction est croissante ou décroissante sur , on dit alors que la fonction est monotone sur . La fonction est dite strictement monotone sur si elle est soit strictement croissante ou strictement décroissante. Remarque Si une fonction est strictement monotone sur I alors elle est nécessairement monotone sur . Mais en général, la réciproque n’est pas vraie c’est-à-dire une fonction monotone sur un intervalle n’est pas nécessairement strictement monotone sur . Exemple Considérons la fonction définie par : Etudier la monotonie de sur Solution Remarquer que conclure que et montrer que pour , ; et est strictement décroissante sur Définition 7 Soit la fonction définie vers . On dit que associe une et une seule image est une bijection si à tout élément et, à tout de on , on associe un et un seul antécédent (A est considérée comme étant le domaine de 5 Critère Soit une fonction définie sur un intervalle et soit l’ensemble des images. Si est continue et strictement monotone sur . De ce fait, admet une réciproque notée alors induit une bijection de qui est une bijection de sur sur . Propriété géométrique Dans un repère orthogonal les courbes représentatives de sont symétriques par rapport à la première bissectrice d’équation et de sa réciproque . O Définition 8 Soit une fonction définie sur un intervalle On appelle limite de la fonction lorsque et soit tend vers pouvant appartenir à . et l’on note le nombre rée tel que pour des valeurs prises par la variable les valeurs très proches de ou , prises par la fonction sont très voisines du nombre c’est-à-dire 6 Remarque Dans les applications ou les calculs rencontrés en ingénierie, il est important de savoir calculer les limites connaissant certaines limites remarquables. Retenons que : Il existe aussi plusieurs formes d’indétermination dont voici une liste : , , , , , Exercice Calculez les limites suivantes Définition 9 Soit une fonction définie sur un intervalle si . Si est continue en tout point de alors et soit . On dit que est continue en est continue sur Exemple Les fonctions : est continue sur et est continue sur 7 NB Soit : avec domaine de . Soit . Si : on a on a Remarque Les propriétés des fonctions continues étudiées dans les classes antérieures demeurent valables. Si est une fonction continue sur et définie et continue sur , alors Théorème Si est une fonction continue sur tel que Si , alors il existe au moins . Exemple . Montrons qu’il existe Soit la fonction tel que sur Solution est continue sur , par conséquent continue sur , alors il existe Prolongement par continuité Soit une fonction définie sur I sauf peut-être en nouvelle fonction coïncide avec . Supposons que . La ( tilde) définie de la manière suivante : sur et continue en est le prolongement par continuité de en Exemple Considérons la fonction définie sur par . admet-elle un prolongement par continuité en 0 ? Solution Comme pour tout on a on en déduit que tend vers en . Elle est donc prolongeable par continuité en et son prolongement est la fonction définie sur pour tout entier par : 8 Définition 10 Soit un intervalle et l’on note et soit . Soit : . On appelle nombre dérivé de la limite : en si elle existe. On appelle nombre dérivé à gauche de de que l’on note , la limite si elle existe du rapport : De même, on appelle nombre dérivé à droite de si elle existe du rapport : de que l’on note , la limite Théorème La fonction est dérivable en si et seulement si elle admet des nombres dérivés à gauche et à droite qui sont égaux : Si . admet de nombre dérivé en tout point de , alors on dit qu’elle est dérivable sur , et la fonction est dite dérivée première de . Théorème Soit une fonction définie et dérivable sur , alors les propositions suivantes sont vérifiées : Si , , alors est croissante sur Si , , alors est décroissante sur Si , alors est strictement croissante sur Si , alors est strictement décroissante sur Rappel Pour deux fonctions et définies sur un intervalle , on a : 9 EXERCICES Exercice 1 Soit , et la fonction définie sur Discuter suivant le paramètre par la continuité de sur Exercice 2 Soit la fonction définie sur Déterminer a et b pour que par soit dérivable en 10 Chapitre 2 Différentielle d’une fonction numérique d’une variable réelle Dans tout ce chapitre les fonctions considérées sont des fonctions numériques de variable réelle. 1-Définition Soit une fonction dérivable en un point Il existe alors un intervalle contenant . On a : et une fonction définie sur tels que : avec d’où : En posant on a : Posons ; on en déduit que : avec La quantité est appelée la différentielle de au point . De façon plus précise on a la définition suivante : Définition : Si une fonction est dérivable en un point l’application linéaire , on appelle différentielle de C’est pourquoi on dit que en est différentiable en si elle est dérivable en ce point. 11 Notation : est l’accroissement de la variable lorsqu’on passe de Le nombre Dans la pratique, est noté est alors et on note : Si on pose et est appelé la différentielle de . La différentielle de , on écrit est dérivable on a : ; . Plus généralement, en tout point et sont respectivement les différentielles de à . en où et . Exemple : Calculer les différentielles des fonctions et telles que : Solution et – – Remarque La différentielle d’une fonction dérivable sur un intervalle est nulle sur si et seulement si, cette fonction est constante sur . II- Différentielle d’une somme, d’un produit, d’un quotient de fonctions Soient deux fonctions et différentiables ; on a les propriétés suivantes : Applications a) Si , , …, sont des fonctions différentiables en un point , on a en ce point : . b) Soit une fonction différentiable et un nombre réel tel que est différentiable. On a: III-Application de la différentielle au calcul approché. 1. Formule d’approximation Soit une fonction différentiable en un point ; la formule (1) du (I-) s’écrit : , avec 12 Or . est l’accroissement de la fonction lorsque la variable varie de à . On a donc : avec Si est assez petit, le terme est négligeable devant . On peut alors écrire : d’où : La formule (2) permet de calculer une valeur approchée de facilement et si on peut calculer . Exemple Soit la fonction telle que Calculer la valeur exacte de calculatrice. En prenant et lorsqu’on assimile en conservant tous les chiffres affichés par la . Calculer les nombres : ; ce dernier nombre permet d’évaluer l’erreur relative commise . Solution a) b) En prenant – = 2 on a ; alors Remarque Dans de nombreux problèmes, la différentielle sert à calculer l’accroissement de certaines grandeurs. Par exemple, la différentielle de mesure radians subit un accroissement est . Alors si un angle de assez petit, alors son sinus subit une variation telle que : . On écrira : 13 EXERCICES Exercice 1 Calculer la différentielle de chacune des fonctions : ; ; Exercice 2 A l’aide d’une différentielle, trouver une valeur approchée avec trois décimales de chacun des nombres X1 et X2 : – – – Exercice 3 Une machine gonfle un ballon de façon continue pendant un laps de temps . A un instant où le diamètre du ballon est de , la vitesse de croissance du rayon est seconde. Quelle est la vitesse de croissance du volume du ballon à l’instant par ? Exercice 4 Un circuit électrique est composé d’un générateur de f.é.m. extérieure ; la résistance intérieure du générateur est accroissement Volts et d’une résistance . Si subit un , calculer les valeurs approchées des variations suivantes : ) é 14 Chapitre 3 Formules de Taylor et de Maclaurin Nous évoquerons les théorèmes sans démonstration. Les fonctions considérées sont des fonctions de vers . 1. Rappels Théorème Soit une fonction définie sur un intervalle ouvert d’extremum sur , alors . Si est dérivable et admet . Définitions Soit un intervalle ouvert contenant de et soit et : On appelle voisinage de , un intervalle très petit. Soit une fonction définie sur un intervalle tel que Soit . . Dans ce cas, une fonction définie sur un intervalle tel que . Dans ce cas, admet un minimum en si est le minimum de . . admet un maximum en si est le maximum de . Condition d’existence de l’extremum d’une fonction Soit une fonction dérivable sur . La condition d’existence de l’extremum de . Soit est la condition nécessaire le point qui réalise cet extremum. La condition est suffisante lorsque: , dans le cas où admet un minimum dans le cas où admet un maximum alors on étudie le signe de Ainsi pour un maximum , admet un minimum . et si , admet . 15 2. Théorème des accroissements finis (théorème de Lagrange) Enoncé : Soit une fonction définie et continue sur un point tel que et dérivable sur Alors il existe La formule (1) est la formule des accroissements finis. Autre façon d’écrire la formule : c ]a, b[ a c b 0ca ba ca 0 1 ba En posant ca et b a h on a ; 0 1, b a h et c a h . ba peut alors s’écrire : La formule On se sert de ce théorème pour établir la formule de Taylor. 3. Théorème de Rolle Soit une fonction continue sur continue sur dérivable sur et vérifiant les conditions suivantes : et Alors il existe un point tel que 4. Formule de Taylor 4.1. Théorème Soit une fonction continue sur un segment continues également sur [a, b] et telle que existe un point avec , admettant des dérivées soit dérivable sur . Alors il tel que : La formule (3) est la formule de Taylor, le dernier terme est le reste de la formule. 16 4.2. Développement d’une fonction par la formule de Taylor Soit une fonction continue, ainsi que ses dérivées un point donné de I. Alors pour tout sur un intervalle . Soit є on a : à l’ordre n au voisinage de La formule (4) est appelée le développement de la fonction . Le dernier terme est le reste du développement. Exemple : Ecrire le développement à l’ordre au voisinage de de la fonction Résolution et puisque , la fonction est dérivable à tout ordre sur . Donc peut être développée à l’ordre 4 au voisinage de 1. Le développement s’écrit : 5. La formule de Maclaurin. Si la formule (4) devient la formule de Maclaurin : avec Exemple : Soit . développement de On déduit que par la formule de Maclaurin à l’ordre . Ainsi le s’écrit: 17 6. Développements limités 1. Activité : Développons la fonction à l’ordre n au voisinage de Pour les dérivées successives de par la formule de Taylor. x ; posons On a donc Sachant que pour tout le développement de au voisinage de s’écrit : Le reste du développement est car On peut donc écrire : avec 18 d’où avec . En écrivant sous cette forme on dit qu’on a écrit un développement limité de la fonction ln à l’ordre . D’une façon plus générale on a la définition suivante. 2. Définition Une fonction admet un développement limité à l’ordre s’il existe ouvert contenant nombres réels , , …, tels qu’au voisinage de au voisinage d’un nombre réel et une fonction définie dans un intervalle on ait : avec 3. Remarque est souvent désignée par O[( - 0)n], ce qui se Dans (6) l’expression lit ‘‘ petit zéro de ( - 0)n ’’ ; o comme dans ‘‘mot’’, doit être considéré comme une fonction et c’est pourquoi on n’écrit pas o( - )n; ce n’est pas un produit. La notation désigne une expression telle que pour on ait : on a ici Avec cette notation le développement limité s’écrit : Nous admettrons la propriété suivante : Propriété : Si la fonction admet au voisinage de admet une dérivée d’ordre au voisinage de au point des dérivées jusqu’à l’ordre 1 continues et , alors elle admet un développement limité d’ordre donné par 19 7. Application au calcul approché Soit Si un développement limité d’ordre une fonction admettant en est assez voisin de , c’est-à-dire si : es assez petit on peut écrire : Par cette formule on approche la fonction par la fonction polynôme L’erreur commise est alors définie par : et on peut déterminer une incertitude sur l’approximation en utilisant la formule de Taylor. Quelques exemples A) Soit la fonction définie par que soit , l’intervalle où est inclus dans peut donc effectuer le développement limité de et est un nombre réel donné. Quel est dérivable sur On à l’ordre 1 au voisinage du nombre zéro. , donc Développement limité : Pour assez petit on a (une approximation du 1er ordre) : L’erreur commise est sensiblement égale à Cette quantité est le 3e terme du développement limité de Pour à l’ordre 2 au voisinage de 0. on a le tableau suivant : Valeur approchée Incertitude 2 -2 -1 20 - B) Fonctions trigonométriques Il s’agit de valeurs approchées pour petit (au 1er ou 2e ordre) (au 3e ordre) Remarque générale Pour fixé, l’approximation est d’autant meilleure que Pour donné, l’approximation est d’autant meilleure que est plus petit. est plus grand Formulaire de quelques développements limités usuels Fonction Développement limité 21 22 EXERCICES Exercice 1 1. Ecrire le développement limité d’ordre 3 au voisinage de -1 de la fonction 2. En utilisant un développement limité d’ordre valeur approchée à trois décimales du nombre au voisinage de , calculer une : Exercice 2 Ecrire les développements limités au voisinage de 0 des fonctions suivantes : à l’ordre 5 ; à l’ordre 4 ; à l’ordre 3 ; à l’ordre 3. Exercice 3 1. Ecrire les développements limités d’ordre au voisinage de des fonctions , 2. Ecrire le développement limité d’ordre 4 au voisinage de ; ; des fonctions : ; Exercice 4 En utilisant la formule de Mac Laurin à l’ordre 3, trouver une valeur approchée de et évaluer l’erreur d’approximation (prendre 23
