1
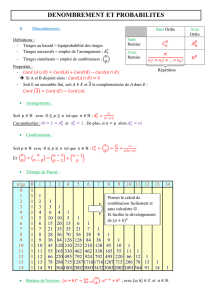
Proba. Solution série n°3 (suite)
Ex. 3
2
3
4
5
1/10
4/10
3/10
2/10
;
;
= E(X^2)-(EX))^2
:
4
9
16
25
1/10
4/10
3/10
2/10
; d’où
Ex. 5
C’est des tirages simultanés ; donc c’est 5 tirages, sans remise, d’une boule. C’est la loi
hypergéométrique.
X suit la loi
ne peut pas être égal à 0 ou 5.
Il faut alors dresser le tableau :
1
2
3
4
4/56
24/56
24/56
4/56
; E(X)=5*0,5=2,5
2
ii- C’est la loi binomiale de paramètres : n=5 ; p=0,5
On effectue 5 tirages d’une boule , que l’on remet à chaque fois. Loi de probabilité :
p(X=k)=…k=0….,5
Ex. 6
X suit la loi géométrique de paramètre 1/6
Y suit la loi géométrique de paramètre 5/6
Loi de X :
Loi de Y :
=
1
/
2
100%
