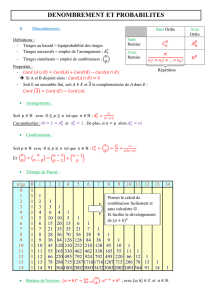
Formulaire TS de Probabilités

AudaScol
AudaScolAudaScol
AudaScol – 1, rue Evariste Galois 11000 Carcassonne – 04 68 25 27 36
Page 1
Formulaires TS : Probabilités
Définitions
Ω
est :
φ
est :
A
est :
A
∪
B se lit :
C’est l’ensemble des éléments :
A
∩
B se lit :
C’est l’ensemble des éléments :
Dénombrement
Lors d’un tirage simultané de p éléments dans un ensemble de n éléments, le nombre de tirages possibles
est :
Lors de tirages successifs sans remise de p éléments dans un ensemble de n éléments, le nombre de tirages
possibles est :
Lors de tirages successifs avec remise de p éléments dans un ensemble de n éléments, le nombre de tirages
possibles est :
Probabilités
p(A) =
..........
..........
p(
Ω
) = p(
φ
) =
∀
A , p(A)
∈
p(
A
) =
p(A
∪
B) =
p(A
∩
B) =
A
p (B) =
A et B sont incompatibles ssi :
⇔
⇔
A et B sont indépendants ssi :
⇔
⇔
Théorème des probabilités totales :
Si A et B forment une …………… de
Ω
, c'est-à-dire si : ……………. et ……………
Alors pour tout événement E, p(E) =

AudaScol
AudaScolAudaScol
AudaScol – 1, rue Evariste Galois 11000 Carcassonne – 04 68 25 27 36
Page 2
Variables aléatoires
Si X est une variable aléatoire discrète (c'est-à-dire ayant un nombre fini de valeurs possibles), alors, la loi
de probabilité de X est : ………………………………………………………………………………
……………………………………………………………………………………………………………..
E(X) s’appelle : et E(X) =
V(X) s’appelle : et V(X) =
σ
(X) s’appelle : et
σ
(X) =
La variable aléatoire X suit une loi binômiale de paramètres : ………………….ssi
-
-
-
-
Dans ce cas : p(X = k) = E(X) = V(X) =
Cas des variables aléatoires continues :
La fonction f est une densité de probabilité sur un intervalle I ssi :
-
-
-
Dans ce cas, p(
[
]
β
α
, ) =
Une loi uniforme sur
[
]
ba, a pour densité de probabilité : f(x) =
Et si
[
]
β
α
,
⊂
[
]
ba, , p(
[
]
β
α
, ) =
Une loi exponentielle (durée de vie sans vieillissement) a pour densité de probabilité :
f(x) =
Et p(X
≤
b) = =
p(
[
]
β
α
, ) = = =
p(X>b) = =>
>
)( bXp
aX