Exercices de Mathématiques Financières : Emprunts et Annuités
Telechargé par
oulay2002

MATHEMATIQUES FINANCIERES
Exercice 1
Un emprunt de 4.000F doit être remboursé au taux de 11% sur 4 ans grâce à des annuités
constantes ; la première intervenant 1an après l’emprunt
1) Calculer le montant de l’annuité
2) Quelle est la loi des amortissements ?
3) Quel est le montant du dernier amortissement ?
4) Construire le tableau d’amortissement relatif à cet emprunt.
Exercice 2
Un emprunt au taux annuel de 5% est remboursable par 6 annuités constantes.
La somme du premier et du dernier amortissement est de 267722,52F.
1) Calculer le premier amortissement.
2) Calculer le capital emprunté.
3) Donner la dernière ligne du tableau d’amortissement.
Exercice 3
Un emprunt est remboursable au moyen d’annuités constantes. On relève entre autre dans
le tableau d’amortissement de cet emprunt les indications suivantes :
Intérêt contenu dans la 4ème annuité : 579494,24F.
Amortissement contenu dans la 4ème annuité : 397954,61F
La différence entre le 4ème amortissement et le 7ème amortissement est de 138978,73F
1) Calculer le montant de la dette initiale.
2) Calculer le nombre d’annuités.
3) Donner les deux dernières lignes du tableau d’amortissement.

Exercice 4
On a relevé les informations suivantes dans le tableau d’amortissement d’un emprunt indivis
effectué au taux i et remboursable à l’aide de n annuités constantes a, la 1ère payable un an
après l’emprunt.
- Les intérêts payés à la fin des 3 dernières années sont respectivement de
723974,81F, 515486,75F et 275725,47F ;
- Le premier amortissement est de 913895,25F
1) Montrer que
))(1()(,2 121 +++ −+=−− kkkk IIiIInk
2) En déduire le taux de l’emprunt i.
3) Calculer le dernier amortissement et l’annuité constante a.
4) Quel est le nombre d’annuités ?
5) Déterminer le capital emprunté D
0
Exercice 5
Un emprunt d’une valeur K, contracté au taux annuel i est remboursable à l’aide de n
annuités constantes a. On donne les informations suivantes tirées du tableau
d’amortissement.
-le 1er amortissement est de 36188,75F
- le capital restant dû à 2 années de la fin des annuités est de 128710,56F
- le dernier amortissement est de 66531,54F
1) Calculer i, a, K, et n
2) Donner la 6ème ligne du tableau d’amortissement
3) Immédiatement après le 6ème versement, le débiteur décide de rembourser les annuités
restantes par des amortissements constants ;
a- Quelle est la valeur de chaque amortissement ?
b- Quelle est la loi des annuités à venir ?
Exercice 6
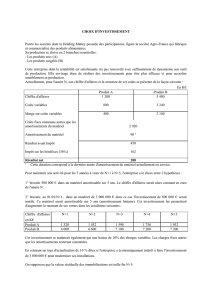
Pour réaliser un investissement, l’entreprise TILA sollicite et obtient d’une banque, un crédit
de 750000F à la fin de l’année 2000.
Cet emprunt remboursable à l’aide d’annuités dont la 1ère intervient à la fin de l’année 2001,
peut être remboursé selon les modalités suivantes :
1ère modalité :
Les annuités de remboursement sont constantes et le capital restant dû après l’annuité de
2006 est égal à l’amortissement de 2007.

Par ailleurs, les informations données par les documents comptables indiquent que jusqu’à
la fin de l’année 2007, le cumul des intérêts payés s’élève à 409502,37F.
1) Calculer l’annuité constante
2) Quel est le taux d’emprunt ?
3) Ecrire la 1ère, la 4ème et la 7ème ligne du tableau d’amortissement.
2ème modalité :
On suppose que le taux de l’emprunt est de 12% l’an, que les intérêts contenus dans les
annuités sont en progression arithmétique de raison r et le nombre d’annuités est 10.
1) Monter que si les intérêts sont en progression arithmétique de raison –D0i/n alors les
amortissements sont constants. Quelle est alors la loi des annuités ?
2) Calculer les annuités et les amortissements de la 1ère, 4ème et 10ème année dans le cas où
r = -9000.
Exercice 7
La société MALO a obtenu d’un établissement financier, un emprunt de 15000F, au taux
annuel i=9%, remboursable à l’aide d’annuités dont la 1ère intervient un an après l’emprunt.
A) On suppose que les annuités de remboursement sont constantes et que la différence
entre le 6ème amortissement et le 1er amortissement est de 878,15F.
1- Quel est le 1er amortissement ?
2- Calculer le nombre d’annuités.
B) On suppose que les amortissements contenus dans les annuités sont en progression
arithmétique de raison 500F et que la 1ère annuité est de 4350F.
1- Donner la 1ère ligne du tableau d’amortissement.
2- En combien de versements peut-on amortir la dette ?
C) On suppose que les amortissements contenus dans les annuités sont en progression
géométrique de raison 1,09 et qu’il y a 5 annuités.
1- Quelle est la loi des annuités ?
2- Monter que i=I3/(A3+D3 )
3- Immédiatement après le 3ème versement, MALO veut se libérer de sa dette
Quelle somme doit-elle alors verser ?

Exercice 8
L’entreprise BONGOSS contracte un emprunt remboursable par annuités constantes.
L’examen du tableau d’amortissement de cet emprunt donne les renseignements suivants :
-Intérêts payés l’avant dernière année : 2785,58F
-Intérêts payés la dernière année : 1435F
-Différence des intérêts payés à la fin des deux 1ère année : 938,75F
1-Montrer que la différence des intérêts payés à la fin de deux années consécutives de rang
k et k+1 est égale à l’intérêt de l’amortissement de rang k.
2- Montrez que le taux d’intérêt de cet emprunt est de 6,25%.
3- Déterminer :
a) Le dernier amortissement.
b) L’annuité constante
c) Le 1er amortissement
d) La somme empruntée.
e) La durée de l’emprunt
4- Présenter les 3 premières lignes du tableau d’amortissement.
Exercice 9
Un emprunt obligataire a les caractéristiques suivantes :
- Nombre d’obligations émises : 30 000.
- Taux nominal 12% l’an.
- Valeur nominal de chaque titre 3000 F.
1) Présenter le tableau d’amortissement dans les 2 cas suivants :
a- Le remboursement au pair se fait à l’aide de 5 annuités constantes.
b- Le remboursement au pair se fait à l’aide de 4 annuités contenant des
amortissements constants.
2) On suppose que le remboursement se fait à 3250F par 5 annuités constantes.
a- Comment évoluent les nombres titres amortis chaque année ?
b- Etablir le tableau d’amortissement
c- Calculer le taux de rendement moyen.

Exercice 10
A)Un emprunt de 10000 obligations de valeur nominale 200F est remboursable au pair par
20 annuités constantes au taux de 4%.
1) Calculer :
a) Le nombre d’obligations à la fin de la 1ère année
b) Le montant de l’annuité théorique
2) Etablir les 3 premières lignes du tableau d’amortissement
B) On considère un second emprunt de 10000 obligations de valeur nominale 200F et
remboursable à 225F par 20 annuités constantes. Les nombres théoriques d’obligations
amorties dès la 1ère année des deux emprunts sont égaux.
1) calculer :
a) Le taux du second emprunt
b) L’annuité théorique du second emprunt.
2) Etablir les deux premières lignes du tableau d’amortissement.
N.B : Pour ces tableaux d’amortissements partiels, on arrondira chaque nombre théorique à
l’entier le plus proche.
Exercice 11
La SMRF( Société de Mobilisation de Ressources Financières) a émis sur le marché, 12000
obligations, de valeur nominale 6000F chacune.
Le coupon annuel payé sur chaque titre est de 420F. Le remboursement est assuré par 5
annuités constantes.
1) On suppose que le remboursement se fait au pair.
a- Quel est le taux nominal de cet emprunt ?
b- Donner la 1ère et la dernière ligne du tableau d’amortissement.
2) On suppose maintenant que le remboursement se fait au dessus du pair et que les
nombres d’obligations théoriques amorties à la 2ème année et à la 4ème année sont
respectivement de 2239,39 et 2550,48.
a- Calculer le taux j pour lequel le coupon se calcule avec la valeur de remboursement R.
b- En déduire cette valeur de remboursement
c- Donner les deux dernières lignes du tableau d’amortissement.
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
1
/
16
100%