télécharger le document

ECES / COURS DE FINANCEMENT DES INVESTISSEMENTS / M. SADIO
1
CHAPITRE 2 : PREPARATION A L’ANALYSE DE RENTABILITE
La démarche pour une méthode d’aide à la décision d’investissement consiste dans un premier
temps à élaborer un ensemble d’hypothèses relatives aux caractéristiques du projet envisagé et
à l’environnement dans lequel il devra prendre place.
Dans un deuxième temps, il s’agit d’utiliser certains outils mathématiques qui indiqueront si le
projet est éligible ou non (si sa rentabilité estimée est suffisante pour qu’il soit retenu) ; ces outils
permettront le cas échéant, de classer par ordre de préférence plusieurs projets en concurrence.
Cette phase préparatoire permet de poser correctement le problème auquel le décideur cherche
à donner une réponse. Elle quantifie les suites prévisibles d’une décision, limite les risques
d’oubli de telle ou telle conséquence et met en lumière d’éventuelles solutions.
I. LES DONNEES D’UN PROJET D’INVESTISSEMENT
I.1 Le capital investi
C’est la dépense que doit supporter l’entreprise pour réaliser le projet. Le capital investi
comprend le coût d’achat du matériel et l’augmentation du besoin de financement de
l’exploitation qui découle de la réalisation du projet.
Le coût d’achat englobe :
• le prix d’achat hors taxe ;
• les frais accessoires (frais de transport, d’installation, etc.) ;
• les droits de douane si le bien est importé ;
• la TVA non récupérable.
Concernant l’augmentation du besoin de financement de l’exploitation, tout projet accroît
généralement l’activité de l’entreprise, ce qui a comme conséquence d’augmenter le BFR
d’exploitation. Ce besoin nouveau appelle un financement nouveau. Ainsi, le capital investi doit
prendre en compte le supplément initial du BFRE lié au projet et les augmentations successives
qui vont s’échelonner sur la durée de vie du projet. En outre, selon le cas, le versement d’une
caution ou le paiement de l’option dans un contrat de crédit bail fait partie des flux
d’investissement.
I.2 La durée de vie du projet
L’évaluation des gains attendus suppose la connaissance de la durée d’exploitation du projet. En
principe, c’est la durée économique qui est retenue. Mais, si elle est difficile à prévoir, on retient
la durée de l’amortissement du bien.
I.3 Les flux de trésorerie générés par le projet
I.3.1 La notion de flux de trésorerie (cash-flows)
L’analyse d’un projet conduit à étudier les flux de trésorerie strictement liés à cet investissement,
en ignorant l’activité d’ensemble de l’entreprise. On parle d’analyse marginale des flux
monétaires.

ECES / COURS DE FINANCEMENT DES INVESTISSEMENTS / M. SADIO
2
Cash-flows = recettes imputables au projet – dépenses imputables au projet
En principe, les cash-flows sont générés de manière continue mais pour simplifier les calculs de
rentabilité, on admet qu’ils sont obtenus à la fin de chaque exercice.
I.3.2 L’évaluation des cash-flows
La plupart des éléments constitutifs des cash-flows sont évalués prévisionnellement. Ces
éléments sont le chiffre d’affaire, les coûts d’exploitation et les impôts.
Si l’on admet qu’il y a égalité entre recettes et chiffre d’affaire d’une part, et entre dépenses et
charges décaissables d’autre part, on en déduit que :
Cash-flows = chiffre d’affaire – charges décaissables
Or, on peut écrire que : résultat net = chiffre d’affaire – (charges décaissables + dotations)
On a donc :
Cash-flows = Résultat net + Dotations
I.3.3 Exemple de calcul de cash-flows
Pour diversifier sa production, une entreprise hésite entre deux projets d’investissement :
! l’acquisition d’un équipement d’occasion A qui nécessite des dépenses d’entretien
annuelles ;
! l’acquisition d’un équipement neuf B.
L’entreprise vous communique des informations sur ces deux projets et vous demande votre
conseil quant au choix à retenir.
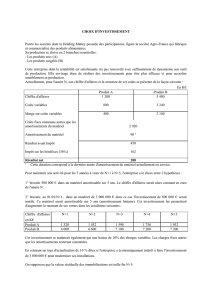
• Caractéristiques des deux projets :
Equipement A
Equipement B
Prix d’achat HT 200 000 300 000
Amortissement sur 5 ans
Linéaire Linéaire
Valeur résiduelle
0 0
• Les dépenses prévisionnelles d’entretien du matériel A sont :
Année
1
2
3
4
5
Montant 10 000 30 000 40 000 40 000 40 000
• Volume prévisionnel des ventes (matériels A et B) :
Année
1
2
3
4
5
Quantité 20 000 50 000 80 000 100 000 100 000
• Prix de vente unitaire : 8 F ; coût de fabrication unitaire (hors amortissement) : 5 F ; taux
d’imposition : 30 %.
Etablir les tableaux de flux de trésorerie des deux projets

ECES / COURS DE FINANCEMENT DES INVESTISSEMENTS / M. SADIO
3
Solution
Tableau des flux de trésorerie du projet 1 (équipement A)
Année 0 1 2 3 4 5
Investissement
200 000
Chiffre d'affaire 160 000
400 000
640 000
800 000
800 000
Charges d'entretien 10 000
30 000
40 000 40 000 40 000
Charges d'exploitation
100 000
250 000
400 000
500 000
500 000
Amortissement 40 000
40 000
40 000 40 000 40 000
Résultat avant impôt 10 000 80 000 160 000 220 000 220 000
Résultat net 7 000 56 000 112 000 154 000 154 000
Flux nets - 200 000
47 000 96 000 152 000 194 000 194 000
Tableau des flux de trésorerie du projet 2 (équipement B)
Année 0 1 2 3 4 5
Investissement
300 000
Chiffre d'affaire 160 000
400 000
640 000
800 000
800 000
Charges d'exploitation
100 000
250 000
400 000
500 000
500 000
Amortissement 60 000
60 000
60 000
60 000
60 000
Résultat avant impôt 0 90 000 180 000 240 000 240 000
Résultat net 0 63 000 126 000 168 000 168 000
Flux nets - 300 000
60 000 123 000 186 000 228 000 228 000
I.3.4 La valeur résiduelle et la récupération du BFRE
I.3.4.1 La valeur résiduelle
Dans le cas général, et bien qu’un projet ait une durée de vie économique supérieure à sa durée
de vie comptable, on retient cette dernière pour l’évaluation du projet. Par contre, à la fin de cette
période, le projet est supposé disparaitre et la valeur de l’immobilisation être nulle (valeur nulle
comptable).
Mais dans certaines conditions, il est possible d’attribuer une valeur marchande résiduelle non
nulle à ce bien. Cette valeur résiduelle en fin d’exploitation est une recette additionnelle qui doit
être prise en compte la dernière année du projet.
Remarque : si on revend le bien, le produit de cession encaissé donne lieu à la détermination
d’une plus-value de cession, laquelle est soumise à l’impôt sur les sociétés. La rentrée nette de
trésorerie sera la différente entre la plus-value de cession et le montant de l’impôt.
I.3.4.2 La récupération du BFRE
En fin de projet, les stocks sont liquidés, les créances clients sont recouvrés et les dettes
fournisseurs réglées. On considère que le besoin en fonds de roulement (BFR initial + BFR
complémentaires) est récupéré.

ECES / COURS DE FINANCEMENT DES INVESTISSEMENTS / M. SADIO
4
I.4 Le taux de rendement minimal
Il correspond au taux de rendement au dessous duquel on renoncerait à effectuer
l’investissement. Différents taux peuvent être retenus :
• le taux que l’on pourrait obtenir si on plaçait sur le marché financier les capitaux
correspondant à l’investissement (coût d’opportunité du capital) ;
• le taux de rendement moyen de ces mêmes capitaux si on les plaçait dans des opérations
dont les risques sont identiques au projet d’investissement envisagé (coût du capital
propre) ;
• le taux de revient des emprunts nécessaires au financement du projet (coût de
l’endettement).
II. LA VALEUR ACTUELLE
La valeur actuelle d’un actif qui génère des cash-flows sur plusieurs périodes correspond à :
VA = CF
1
x (1+ r
1
)
-1
+CF
2
x (1+ r
2
)
-2
+ …… + CF
n
x (1 + r
n
)
-n
Où CF
i
: cash-flow de l’année i ; r
i
: taux d’actualisation de l’année i
Le taux d’actualisation à utiliser est le taux de rentabilité minimum de l’entreprise.
Théoriquement, ce taux représente le coût des capitaux utilisés par l’entreprise.
Les cash-flows sont actualisés pour deux raisons : un franc aujourd’hui vaut plus qu’un franc
demain et un franc risqué vaut moins qu’un franc sûr.
La VAN est la différence entre les cash-flows actualisés sur la durée de vie du projet et les
capitaux investis. On obtient la Valeur Actuelle Nette (VAN) en ajoutant à la Valeur Actuelle le
cash-flow initial (généralement négatif).
Exemple 1 : Calculons les VAN des projets de l’exemple précédent au taux de 12%
VAN
1
= -200 000 + 47 000 x 1,12
-1
+ 96 000 x 1,12
-2
+ 152 000 x 1,12
-3
+ 194 000 x 1,12
-4
+
194 000 x 1,12
-5
= 260 057 F
VAN
2
= -300 000 + 60 000 x 1,12
-1
+ 123 000 x 1,12
-2
+ 186 000 x 1,12
-3
+ 228 000 x 1,12
-4
+
228 000 x 1,1
-5
= 258 289 F
Exemple 2 :
Pour un projet immobilisé, l’entrepreneur vous annonce que la construction prendra deux ans et
vous demande d’étaler vos versements comme suit :
1. un versement initial de 100 000 euros (vous devez aussi payer immédiatement le terrain
pour 50 000 euros) ;
2. un versement de 100 000 euros à la fin de la première année, un versement de
100 000 euros lorsque l’immeuble pourra être occupé, à la fin de la deuxième année.
Votre conseiller en immobilier vous assure que l’immeuble vaudra 400 000 euros lorsqu’il sera
achevé.

ECES / COURS DE FINANCEMENT DES INVESTISSEMENTS / M. SADIO
5
Calculer la VAN des cash-flows de ce projet à un taux de 7%.
VAN = CF
0
+ CF
1
/ (1+r
1
) +CF
2
/ (1+r
2
)
2
CF
0
= -100 000 – 50 000 = -150 000
CF
1
= -100 000
CF
2
= -100 000 + 400 000 = 300 000
VAN = -150 000 – 100 000 x 1,07
-1
+ 300 000 x 1,07
-2
VAN = 18 400 euros
III. SYSTEMES D’EMPRUNTS INDIVIS LES PLUS USITES
III.1 Emprunts remboursables en une seule fois ou in fine
L’emprunteur ne paie, à la fin de chaque période que l’intérêt du capital emprunté. Il rembourse
en une seule fois, à l’époque fixée dans le contrat, l’intégralité du capital emprunté.
Les annuités successives sont égales à V
0
i à l’exception de la dernière qui comprend le
remboursement du capital a
n
=V
O
+V
0
i
Remarque : pour rembourser l’emprunt, on peut par exemple placer sur un produit de
capitalisation, auprès du même établissement financier, une certaine somme dont la valeur
acquise à la date n est égale au montant de l’emprunt. On dit qu’on adosse l’emprunt. On peut
aussi verser sur un fonds d’amortissement des sommes dont la valeur acquise à la date n est
égale au montant de l’emprunt.
III.2 Emprunts à amortissements constants
Le capital emprunté est remboursé en n périodes par amortissements égaux chacun à V
O
/ n.
Deux annuités consécutives quelconques sont définis : a
k+1
= a
k
– (V
O
/ n)i.
Exemple :
Dresser le tableau d’amortissement d’un emprunt de 700 000 F remboursable en 5 ans par
annuité comportant un amortissement constant, la première annuité échéant un an après la
remise des fonds. Taux d’intérêt : 6,5 %.
Année Capital restant dû (début
de période) Intérêt Amortissement
Annuité
1 700 000 45 500 140 000 185 500
2 560 000 36 400 140 000 176 400
3 420 000 27 300 140 000 167 300
4 280 000 18 200 140 000 158 200
5 140 000 9 100 140 000 149 100
III.3 Emprunts remboursables par annuités constantes
L’emprunteur paie, à la fin de chaque période, une annuité constante. La formule de la valeur
actuelle d’une suite d’annuité constante est V
O
= a x [(1-(1 +i)
-n
) / i].