ccndl-2nde-cd-mathematiques-2012-2013-composition-de-fin-du-2e-trim

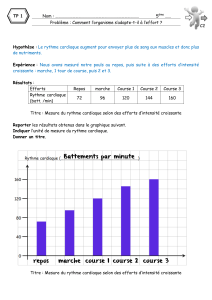
PPJ JOEL
frikbook
G.H.A
DIOCESE DE PORTO-NOVO Année Scolaire : 2012 - 2013
COLLEGE CATHOLIQUE COMPOSITION de FIN du 2
ème
Tri.
NOTRE DAME DE LOURDES Classe : 2
nde
CD
01 BP : 900 Tél : [phone] Durée : 3 heures
EPREUVE DE MATHEMATIQUES
Contexte
Vignon est un élève studieux et très intelligent de la classe de seconde
scientifique au collège ‘’Les Intègres ‘’.
N’ayant pas de livre de mathématiques, il est toujours à la recherche
d’exercices pour son entraînement .C’est dans cette optique qu’il passe, dans les
autres classes de sa promotion après les cours de mathématiques pour
s’imprégner de ce qui a été fait et prend note si cela l’intéresse.
Voici, sa prise de notes dans une classe après leur dernier cours de la
semaine dernière. On considère les fonctions f, g, h, et k telles que :
2
2
: :
1 1
1
2 3
:
( 1)
1
g IR IR h IR IR
x x x
x
k IR IR
x
x
x
® ®
+
+
®
-
-
a a
a
Il veut s’en servir pour préparer son prochain devoir de mathématiques.
Tâche
Tu es invité(e) à résoudre les problèmes suivant en compagnie de Vignon en
utilisant tes connaissances en mathématiques.

PPJ JOEL
frikbook
Problème 1
1.- Détermine l’ensemble de définition de f.
2.- Détermine l’image par f des nombres -4 ; 2 et 9.
3.- a) Donne le sens de variation de f.
b) Donne l’allure d’une courbe lisse représentant f dans un repère (O,I,J)
Problème 2
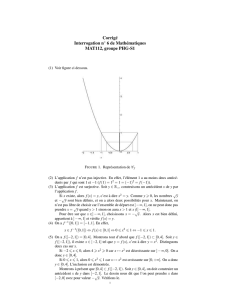
(C) est la représentation graphique de g dans le repère (O, I, J).
4.- a) Résous dans IR, l’inéquation
2 3 0
x
+ ³
.
b) Déduis-en le domaine de définition D de g
5.- a) Détermine, lorsqu’elle existe, l’image par g de chacun des nombres
réels : -2 ; 1 et 0.
b) Détermine l’antécédent par g du nombre 1.
6.- a) Parmi les points suivants, indique ceux qui appartiennent à
(C) :
5 1
(1; ) ; ( 1;2) ; (3; )
5 3
A B E-
b)
1
( ; )
2
k a
est un point de (C). Détermine le réel a.
7.- a) Détermine l’ensemble de définition de chacune des foncions h et k.
b) Démontre que h et k coïncident sur
]
[
1;
+ ¥
.
Problème 3
Vignon veut aller loin en ce qui concerne le sens de variation d’une fonction.
Tu feras comme lui en répondant aux questions ci-après.
Soit une fonction définie sur
[
]
;
a c
et b un réel de l’intervalle.
8.-Démontre que si f est croissante sur
[
]
;
a b
et croissante sur
[
]
;
b c
alors f est
croissante sur
[
]
;
a c
.

PPJ JOEL
frikbook
9.- Soit j la fonction définie sur
[
]
0;10
par
[ ]
[
]
1 0;4
( )
2 3 4;10
x si x
j x x si x
ì
ï+ Î
ï
=í
ï- Î
ï
î
a) justifie que j est une fonction affine par intervalles.
b) quel est le sens de variation de j sur [0 ; 4] ? sur [4 ; 10].
j est –elle croissante sur [0 ; 10] ?