exercice-corrige-en-regime-sinusoidal-monophase

Exercice corrigé en régime sinusoïdal monophasé
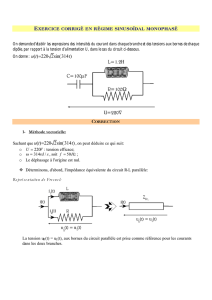
On demande d’établir les expressions des intensités du courant dans chaque branche et des tensions aux bornes de chaque
dipôle, par rapport à la tension d’alimentation U, dans le cas du circuit ci-dessous.
On donne : )314sin(2220)( ttu=
Correction
1- Méthode vectorielle:
Sachant que )314sin(2220)( ttu=, on peut déduire ce qui suit:
o VU220
=
: tension efficace;
o srd /314
=
ω
, soit
Hz
f
50
=
;
o Le déphasage à l'origine est nul.
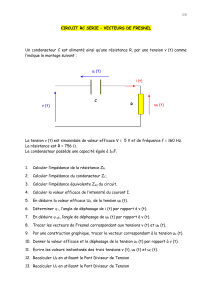
v Déterminons, d'abord, l'impédance équivalente du circuit R-L parallèle:
Représentation de Fresnel:
La tension uR(t) = uL(t), aux bornes du circuit parallèle est prise comme référence pour les courants
dans les deux branches.

Ce qui nous permet de tracer le graphique suivant:
Nous avons donc:
LRIII
r
r
r
+= et par conséquent: 222 LRIII +=
Soit : 2
2
2
2
2
2
2
2
)( ωL
U
R
U
Z
U
Z
ULL
RL
L
RL
R+==
D'où,
- module:
sY
LRZRL
RL
010346,0
)( 111
22 ==
+= ω et Ω== 65,96
1
RL
RL Y
Z
- déphasage de
I
r
par rapport à R U
r
:
°−= −= −= 86,14
)/(ω
ϕL
R
arctg
I
I
arctg R
L
UIZ
RL
Zpeut s'écrire, alors: °+Ω=86,1465,96
RL
Z
v Déterminons, ensuite, l'impédance équivalente totale:

Le circuit est composé d'une impédance RL Z en série avec une capacité C. Le courant leur est donc
commun, dans la représentation de Fresnel ce dernier sera pris comme référence.
Nous avons:
CZUUU
r
r
r
+=
D'où:
- Module:
(
)
CZCZCZUUUUUUU
r
r
,cos2
222 ++=
Ce qui nous permet d'écrire, en simplifiant par
I
:
(
)
CZCRLCRL UUZZZZZ
r
r
,cos2
222 ++=
Soit
(
)
CZCRLCRL UUZZZZZ
r
r
,cos2
22 ++=
Sachant que °=+= 86,10490),(ZCZUU ϕ
r
r
et Ω=== 85,31
1
ω
C
XZCC
Ω
=
7
,
93
Z
- Déphasage de U par rapport à I:
On a:
CZZ UUU −= ϕϕ sinsin
Ou encore:
CZRL ZZZ −= ϕϕ sinsin
Soit
−
=Z
ZZ CZRL ϕ
ϕsin arcsin

°
−
=
32
,
4
ϕ
: L'impédance totale est de type capacitive, la tension est en retard sur le courant.
°−Ω=32,47,93Z
v Détermination des grandeurs partielles :
v Détermination du l'intensité du courant total:
A
Z
U
I35,2
7,93
220 ===
Le déphasage de entre
I
r
et U
r
est
rd
075
,
0
32
,
4
=
°
=
ϕ
, le courant est en avance sur la tension.
L'intensité du courant instantané
)
(
t
i
s'écrit:
)075,0314sin(235,2)( += tti
v Détermination de la tension aux bornes de RL Z:
VIZURLZ13,22735,265,96 =×==

Son déphasage par rapport à
I
est rd
Z26,086,14 −=°−=ϕ
Sachant que le déphasage entre
I
et U est
ϕ
, le déphasage de Z Upar rapport à Uest
rd
Z33,018,1986,1432,4)( =°=+=+− ϕϕ
La tension instantanée )(tuZs'écrit:
)33,0314sin(213,227)( += ttuZ
v Détermination de l'intensité du courant dans la résistance
R
:
A
R
U
IZ
R27,2
100
13,227 ===
Sachant que le courant R I
r
et la tension Z U
r
sont en phase, l'intensité du courant instantané s'écrit:
)33,0314sin(227,2)( += ttiR
v Détermination de l'intensité du courant dans l'inductance
L
:
A
L
U
IZ
L6,0
8,37613,227 === ω
Sachant que le courant L I
r
est en quadrature de phase retard sur Z U
r
et R I
r
, le déphasage de L I
r
par rapport à
U
r
est: rd
Z24,182,7018,1990)32,486,14(90)(90 −=°−=+−=−−−−=+−°−ϕϕ
L'intensité du courant instantané )(tiLs'écrit:
)24,1314sin(26,0)( −= ttiL
v Détermination de la tension aux bornes de C:
V
e
C
I
UC84,74
314
100
35,2
6=
×
== −
ω
Sachant que la tension C U
r
est en quadrature de phase arrière sur le courant
I
r
, son déphasage par rapport
à U
r
est:
rd
5
,
1
68
,
86
90
32
,
4
90
−
=
°
−
=
−
=
°
−
ϕ