Première S Tout le chapitre 5 : Nombre dérivé

Première S
Tout le chapitre 5 : Nombre dérivé
________________________________________________________________
_________________________________________________________________________________________________________________
toutchap5 1/3
SOMMAIRE
V. 1.ACTIVITES................................................................................................................................................... 2
0.VERIFIER LES ACQUIS P.56 ............................................................................................................................... 2
1. A1 P.58 ........................................................................................................................................................... 2
2. A2 P.58 ........................................................................................................................................................... 2
3. A3 P.59 ........................................................................................................................................................... 2
V. 2. NOMBRE DERIVE ET TANGENTE....................................................................................................... 2
RAPPEL : TAUX DE VARIATION ............................................................................................................................ 2
Définition....................................................................................................................................................... 2
NOMBRE DERIVE DE FEN A .................................................................................................................................. 2
Définition....................................................................................................................................................... 2
Exemples........................................................................................................................................................ 2
EXERCICE 1......................................................................................................................................................... 2
INTERPRETATION GRAPHIQUE : TANGENTE A UNE COURBE ................................................................................. 2
Définition....................................................................................................................................................... 2
EXERCICE2:......................................................................................................................................................... 3
EXERCICE 3 : LIRE UN NOMBRE DERIVE............................................................................................................... 3

Première S
Tout le chapitre 5 : Nombre dérivé
________________________________________________________________
_________________________________________________________________________________________________________________
toutchap5 2/3
V. 1.Activités
0.Vérifier les acquis p.56
1. A1 p.58
2. A2 p.58
3. A3 p.59
V. 2. Nombre dérivé et tangente
Rappel : taux de variation
Définition
Soit f est une fonction définie sur un intervalle I contenant a et a + h avec h non nul. Le rapport f(a + h) – f(a)
hest
appelé taux de variation de f entre a et a + h
Nombre dérivé de fen a
Définition
Soit f est une fonction définie sur un intervalle I contenant a et a + h avec h non nul. La fonction f est dite
dérivable en a si et seulement si f(a + h) – f(a)
h tend vers un réel L lorsque h tend vers 0.
L est appelé nombre dérivé de f en a et on le note f ‘(a).
i.e.lim
h→0 f(a + h) – f(a)
h = f ‘ (a)
NB : en physique, on note : ∆f = f(a + h) – f(a) et ∆x = a + h – a = h d’où ∆f
∆x = f(a + h) – f(a)
h → f ‘ (a)
Exemples
Un point mobile M à l’instant t positif ou nul, a parcouru la distance d(t) = t². Alors sa vitesse moyenne entre
l’instant 4 et 4 + h avec h > 0 est d(4 + h) – d(4)
h = (4 + h)² - 4²
h = 8h+ h² h = 8 + h
Or lim
h→0 (8 + h) = 8. Le nombre dérivé de d en 4 est 8. Soit ici comme, d’(t) = v(t) = 8
Exercice 1
Calcul d’un nombre dérivé
Soit f définie sur R par f(x) = x² - 2x – 1. Montrer que f est dérivable en x = 3 et calculer f ’(3)
f(3 + h) = (3 + h)² - 2(3 + h) – 1 = 9 + 6h + h² - 6 – 2h – 1 = h² + 4h + 2; f(3) = 3² - 2×3 – 1 = 9 – 6 – 1 = 2
f(3 + h) - f(3) = h² + 4h
d’où lim
h→0 f(3 + h) – f(3)
h = lim
h→0 h² + 4h
h = 4. La fonction est dérivable en x = 3 et f ‘(3) = 4
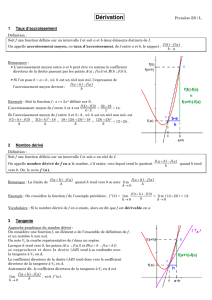
Interprétation graphique : tangente à une courbe
Soit C la courbe représentative d’une fonction f et les points A et M de C d’abscisses respectives a et a + h
f(a + h) – f(a)
h représente le coefficient directeur de la droite (AM).
Dire que f(a + h) – f(a)
h tend vers f ‘(a) quand h tend vers 0 signifie que le coefficient directeur de (AM) tend
vers f ‘(a).
Autrement dit, quand M tend vers A sur la courbe, les droites (AM) tendent vers une position limte qui est la
droite TA passant par A et de coefficient directeur f ‘(a)
Définition
Soit f est une fonction dérivable en a et C sa courbe représentative. La droite passant par A (a ; f(a)) et de
coefficient directeur f ‘(a) est appelé tangente à C en A.
Une équation de cette tangente est donc : y = f ‘(a) ( x – a ) + f(a)

Première S
Tout le chapitre 5 : Nombre dérivé
________________________________________________________________
_________________________________________________________________________________________________________________
toutchap5 3/3
Exercice2:
Avec données de l’exercice 1. Tracer C et la tangente à C en A(3 ;f(3))
La courbe est une parabole tournée vers le haut, de sommet S ⎝
⎜
⎛
⎠
⎟
⎞
-b
2a
f⎝
⎛⎠ ⎞
-b
2a
soit S (1 ; -2) d’où la courbe…
Alors la tangente à C en A(3 ;f(3) = 2) a pour coefficient directeur f ‘(3) = 4
NB : l’équation est donc y = f ‘(a) ( x – a ) + f(a) soit y = f ‘(3) ( x – 3 ) + f(3) c'est-à-dire y = 4 ( x – 3 ) + 2
Donc y = 4x - 10
234567-1-2-3
2
3
4
5
6
-1
01
1
x
y
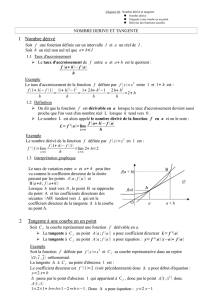
Exercice 3 : lire un nombre dérivé
Lire f ‘(-4) ; f ‘(1) et f ‘ (8) On lit : 1,5 puis -0,25 et 0
23456789101112-1-2-3-4
2
3
4
5
6
7
8
9
-1
-2
01
1
x
y