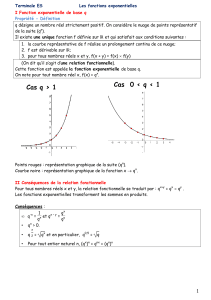
e `f x = `f x = 2 x f x xe =

FICHE DE MEMORISATION EXPONENTIELLES TES
A quelles conditions
une
fonction
f
est une
fonction exponentielle
de base
0
q
?
Quelle est la
relation fonctionnelle
d
es fonctions
exponentielles
?
Que distingue la fonction
exponentielle des
autres fonctions
exponentielles
?
e
…
0
e
… 1
e
… 1 e …
1
2
e
…
x y
e
… x y
e
…
x
e …
n
x
e …
exp'
x
…
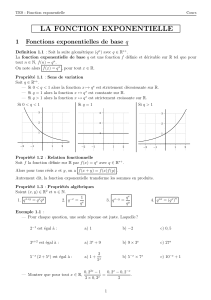
Donner l’allure de
la courbe
représentative de la fonction
exponentielle.
Et donner le tableau de variation.
Si
( )
( )
u x
f x e
, alors
'
f x
…
En particulier,
s
i
2
3 1
( ) x f x e
,
alors
'
f x
…
Donner deux relations entre la
fonction exponentielle et la
fonction logarithme
népérien.
Si
'e
u
f u
alors
f
admet
pour
primitive
…
Par exemple, si
f
est définie par
2
2
x
f x xe
alors
une primitive
de
f
sur
est
…

FICHE DE MEMORISATION EXPONENTIELLES TES
A quelles
conditions une fonction
f
est une
fonction exponentielle
de base 0q ?
La courbe représentative de
f
est le prolongement continu
du nuage de
points représentatif de la suite
n
n
q
f est dérivable sur 
Pour tous réels
et x y
on a
:
f x y f x f y 
Quelle est la
relation fonctionnelle
d
es fonctions exponentielles
?
Pour tous réels
et x y
on a
:
f x y f x f y 
Que distingue la fonction
exponentielle des autres fonctions
exponentielles
?
Sa dérivée en 0 vaut 1. Autrement dit,
exp' 0 1.
e
…
2, 718e
0
e… 1 e… 1
e…
1
2
e… 01e 1
e e 11
e
e
1
2
e e
x y
e… x y e…
x
e…
n
x
e…
x y x y
e e e
x
x y
y
e
ee
 1 x
x
ee
n
x nx
e e
exp' x… exp' x x e
Donner l’allure de
la courbe
représentative de la fonction
exponentielle.
Et donner le tableau de variation.
Si
( )
( ) u x f x e
, alors
'
f x
…
En particulier,
s
i
2
3 1
( ) x f x e 
,
alors
'f x …
( )
' '( )
u x
f x u x e
2
3 1
'( ) 6 x f x xe 
Donner deux relations entre la
fonction exponentielle et la
fonction logarithme népérien.
Pour tout réel
0x
,
ln x
e x
Pour tout réel
x
,
ln x e x
Si
'eu f u
alors
f
admet pour
primitive
…
Par exemple, si fest définie par
2
2x f x xe
alors
une primitive
de
f
sur
est
…
Si
'eu f u
alors
f
admet pour
primitive
la fonction F définie par
eu F
.
Une primitive de fsur  est F : 2
x
x e.