Fonctions exponentielles

Séquence 4
Fonctions
exponentielles
Objectifs de la séquence
Introduire les (nouvelles) fonctions exponentielles
Connaître
des propriétés (équation fonctionnelle, variations, fonction dérivée, …) de
la fonction exponentielle de base e.
Sommaire
1. Pré-requis
2. Introduction aux fonctions exponentielles
3. La fonction exponentielle de base e
4. Dérivation et fonction exponentielle (base e)
5. Synthèse de la séquence
6. Exercices de synthèse
Séquence 4 – MA01
1
© Cned - Académie en ligne
1 Pré-requis
Peut-être avez-vous déjà entendu une personne dire : « La croissance est exponentielle ; il faut réagir vite avant que le phénomène n’atteigne des proportions
trop extravagantes. »
Les mots employés reflètent l’augmentation d’un phénomène à une vitesse extrêmement rapide, s’agissant d’une variation au cours du temps.
Nous allons étudier dans ce chapitre des fonctions dont les valeurs f(x) grandissent très vite (nous préciserons) lorsque la variable x augmente. Rien d’étonnant
à ce qu’on les appelle des fonctions… exponentielles.
A
Exercice
Suites géométriques
Un nénuphar est placé le 1er juin dans un étang de forme carrée de côté 100 m.
Initialement, il couvre 1 m². Chaque jour, il double de taille. On note un la superficie (en m²) couverte par le nénuphar au bout de n jours.
Justifier que la suite (u ) est géométrique.
n
En déduire l’expression de u en fonction de n.
n
Etudier le sens de variation de (u ).
n
Quelle est la surface couverte par le nénuphar au bout d’une semaine ?
Au bout de combien de jours le nénuphar couvrira-t-il :
la
moitié de l’étang ?
la totalité de l’étang ?
Solution
On sait que u = 1.
0
Au bout d’un jour, il couvrira 2 × 1 = 2m² donc u1 = 2. Si le n − ième jour il couvre
une surface de un m², le jour suivant il couvrira une surface de 2 × un m2 autrement dit, un +1 = 2un . Cette relation de récurrence, valable pour tout n ∈
montre que la suite (un ) est géométrique de raison 2.
Comme son premier terme est u = 1 , on en déduit que pour tout n ∈, un = 2n.
0
Séquence 4 – MA01
3
© Cned - Académie en ligne
Puisque la raison de la suite (u ) est strictement supérieure à 1 et que son 1er
n
terme est strictement positif, cette suite est croissante.
Au bout de 7 jours, le nénuphar couvre u = 27 = 128 m2.
7
L’étang a une superficie de 100 × 100 = 10000 m2.
13
On calcule u12 = 212 = 4096, u13 = 2 = 8192 et u14 = 214 = 16384.
Par conséquent, c’est le 13e jour que la taille du nénuphar dépassera la moitié de
l’étang et le jour suivant (le 14e) qu’il couvrira la totalité de l’étang.
Exercice
Solution
Une dame âgée se rappelle qu’une baguette de pain coûtait 0,70 € en 2000 et
que, depuis, son prix a augmenté chaque année du même pourcentage. En 2011,
elle paye 1,20 € à la boulangère. Chaque année, par combien a été multiplié le
prix d’une baguette de pain ?
)
Notons un le prix (en €) de la baguette de pain en ( 2000 + n . Notons aussi q le coefficient par lequel a été multiplié le prix de la baguette chaque année. On a donc u 0 = 0, 7 puis u1 = 0, 7 × q ; ensuite u 2 = 0, 7 × q 2 , … enfin,
u11 = 0, 7 × q 11. Par conséquent, 0, 7 × q 11 = 1, 2.
1
 1, 2  11
D’où q =   1, 05 (ce qui correspond à une augmentation annuelle de 5 %).
 0, 7 
Exercice
Vrai ou faux ?
u
Si n +1 est constant pour tout entier n ∈ alors (u ) est une suite géométrique.
n
un
Si (u ) est une suite géométrique de raison q alors pour tous entiers n et p,
n
un = u p × q n − p .
Dans un pays, on note t N le taux de natalité, t M le taux de mortalité et un le
nombre d’habitants n années après l’an 2000.
Si t = 10 ‰ et t = 10 ‰ alors
N
M
lim un = +∞.
n →+∞
Si t = 12 ‰ et t = 8 ‰ alors (u ) est une suite géométrique de raison
N
M
n
q > 1.
Si t = 9 ‰ et t = 11 ‰ alors (u ) est une suite géométrique de raison
N
M
n
q < 1.
4
© Cned - Académie en ligne
Solution
un + 1
= q implique que pour tout n ∈, un +1 = qun ; la suite (un ) est donc
un
une suite géométrique de raison q.
Séquence 4 – MA01
Etudions d’abord l’égalité à démontrer dans des cas simples.
Lorsque
n = p , l’égalité à démontrer s’écrit un = un q 0 , ce qui est bien vrai.
Lorsque
n = p + 1, l’égalité à démontrer s’écrit un +1 = un q : on reconnaît la
relation de récurrence caractéristique d’une suite géométrique, qui est vraie.
Lorsque n
= p + 2, l’égalité à démontrer s’écrit un + 2 = un q 2 . Cette égalité est
encore vraie puisque la suite (un ) est géométrique donc un + 2 = qun +1 et
un +1 = qun ; d’où un + 2 = qun +1 = q (qun ) = q 2un .
Plus
généralement, si n > p , on peut écrire de proche en proche :
un = q × un −1 = q × q × un − 2 = q × q × q × un − 3 = ...
3 facteurs
3
… = q × q × ... × q × un − (n − p ) = q n − p × u p
n − p facteurs
n −p
ce qui prouve que un = u p × q n − p .
Remarquons enfin que les lettres n et p jouent un rôle symétrique dans l’égalité à dé-
montrer. Par conséquent, si n < p , c’est que p > n donc en échangeant les lettres
n et p on peut écrire l’égalité démontrée au point précédent : u p = un × q p − n
et en divisant chaque membre par q p − n (qui est ≠ 0 car q ≠ 0 ) on obtient
up
1
= un , c’est-à-dire u p q n − p = un (puisque
= q −k ) et l’égalité souhaik
p −n
q
q
tée est ainsi démontrée.
D’une
année sur l’autre la population est multipliée par

10  
10 
 1+ 100  ×  1− 100  = 0, 99 ; autrement dit, pour tout n ∈ on peut
écrire un +1 = 0, 99 × un ce qui prouve que la suite (un ) est géométrique de
raison 0,99.
Conformément à l’étude faite à la séquence 1, portant sur les limites des suites
géométriques, nous commençons par repérer que la suite (un ) est de raison
strictement positive et de premier terme strictement positif. Comme sa raison
q = 0, 99 vérifie 0 < q < 1 , on peut affirmer que lim un = 0.
n →+∞
De manière similaire, on montre que la suite (u ) est géométrique de raison
n
q = 1,12 × 0, 92 = 1, 0304 > 1.
Séquence 4 – MA01
5
© Cned - Académie en ligne
Là encore on montre que la suite (u ) est géométrique. Sa raison est
n
q = 1, 09 × 0, 89 = 0, 9701 < 1.
Remarque
Nous avons rencontré l’ensemble qui est celui des entiers naturels ; on retient
{
}
que = 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; ... ; 127 ; ... .
Dans la suite, nous aurons aussi besoin de l’ensemble des entiers relatifs qu’on
obtient en ajoutant aux nombres de l’ensemble , leurs nombres opposés.
On retiendra que :
{
}
= ... ; − 451 ; ... ; − 4 ; − 3 ; − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 ; ... ; 451 ; ...
Nous utiliserons aussi l’ensemble des nombres réels ; on retiendra que cet ensemble contient tous les nombres connus en classe de terminales ES.
A savoir
Lorsque (un ) est une suite géométrique de raison q, pour tous entiers n et
p, un = u p × q n − p .
Pour démontrer qu’une suite (un ) est géométrique, on peut commencer par
u
calculer n +1 .
un
B
Quelques fonctions particulières
1. Fonctions usuelles
Nom
f (x )
Ensemble de définition
Sens de variations
Carré
f (x ) = x 2
Df = Décroissante sur ] − ∞; 0]
Cube
f (x ) = x 3
Df = Croissante sur Racine carrée
f (x ) = x
Df = [0 ; + ∞ [
Croissante sur [0 ; + ∞ [
Df = ] − ∞ ; 0[∪]0 ; + ∞ [
Décroissante sur ] − ∞; 0[
Inverse
6
© Cned - Académie en ligne
f (x ) =
Séquence 4 – MA01
1
x
Croissante sur [0 ; + ∞ [
Décroissante sur ]0 ; + ∞ [
2. Fonctions polynômes du second degré
Elles
sont définies sur par g ( x ) = ax 2 + bx + c où a , b ,c sont trois réels et
a ≠ 0 (car sinon, g ( x ) = bx + c , c’est-à-dire que g serait une fonction affine).
courbe Cg de g est une parabole dont on calcule l’abscisse α du sommet
en résolvant g ′( x ) = 0 (car au sommet la tangente à la courbe Cg est hori-
La
zontale donc son coefficient directeur est égal à 0).
a > 0 alors g est décroissante sur ] − ∞ ; α ] et croissante sur ]α ; + ∞ [
(« bol tourné vers le haut »).
Si
a < 0 alors g est croissante sur ] − ∞ ; α ] et décroissante sur ]α ; + ∞ [
(« bol tourné vers le bas »).
Si
Exercice
Solution
Déterminer les variations de la fonction f définie sur par f ( x ) = − x 2 + 3x − 5.
f est une fonction polynôme du second degré où (avec les notations ci-dessus)
a = −1 ; b = 3 ; c = −5.
L’abscisse α du sommet de la courbe Cf est solution de l’équation f ′( x ) = 0. On
3
calcule f ′( x ) = −2x + 3 puis on résout f ′( x ) = 0 ⇔ − 2x + 3 = 0 ⇔ x = ,
2
donc α = 1, 5.
Conclusion : f est croissante sur ] − ∞ ; 1, 5] et décroissante sur [1, 5 ; + ∞ [. Elle
atteint son maximum en x = 1, 5 et ce maximum est égal à f (1, 5) = −2, 75 (c’est
l’ordonnée du sommet de la parabole).
C
Dérivation
1. Nombre dérivé ; interprétation graphique
Définition 1
Soit f une fonction définie sur un intervalle I. Soit a ∈I . Si le taux de variation de f entre a et a + h a une limite finie lorsque h tend vers zéro, on dit
que f est dérivable en a. Cette limite est alors appelée nombre dérivé
de f en a.
Elle est notée f ′(a ).
f (a + h ) − f (a )
f ′(a ) = lim
h
h →0
Séquence 4 – MA01
7
© Cned - Académie en ligne
Interprétation graphique
(à bien connaître)
y
f'(a) (unités
ordonnées)
f (a)
1 (unité
abscisses)
Ꮿf
x
O
1 (T)
Si f est dérivable en a, la courbe f
admet une tangente T non parallèle
à l’axe des ordonnées au point d’abscisse a et le coefficient directeur de
cette droite est f ′(a ):
a
Ne pas confondre f (a ) et f ′(a ).
f (a ) est l’ordonnée du point de f
d’abscisse a.
f ′(a ) est le coefficient directeur de
la tangente à f au point d’abscisse a.
Propriété
Soit f une fonction dérivable en un réel a.
La tangente à f au point d’abscisse
a
a pour équation :
y = f ′(a )( x − a ) + f (a )
Remarque
On voit sur cette équation deux renseignements caractérisant la tangente T (qui
est une droite !) :
T a pour coefficient directeur f ′(a ).
En effet, après développement du terme f ′(a )( x − a ) , le coefficient du terme en x
est bien f ′(a ).
(
)
T passe par A a ; f (a ) .
En effet, si on remplace x par a dans cette équation, on obtient :
y = f ′(a )(a − a ) + f (a ) = 0 + f (a ) = f (a ).
8
© Cned - Académie en ligne
Séquence 4 – MA01
2. Fonction dérivée ; formulaire
A savoir
Fonction f
Dérivée f ’
f ( x ) = c (c est une constante)
f ′( x ) = 0
f ( x ) = mx + p
f ′( x ) = m
f (x ) = x 2
f ′( x ) = 2x
f (x ) = x 3
f ′( x ) = 3x 2
f ( x ) = x n , n ∈ − { 0 }
f ′( x ) = nx n −1
f (x ) = x
1
f (x ) =
x
Exercice
Solution
f ′( x ) =
Intervalle I
I =
1
I = 0 ; + ∞ 
2 x
f ′( x ) =
−1
x2
I =  −∞ ; 0 
ou
I = 0 ; + ∞ 
Déterminer une équation de la tangente à la courbe représentant la fonction
« carré » au point d’abscisse 1. En déduire une valeur approchée de 1, 0012.
Ici, f est la fonction est définie sur l’intervalle I = par : f ( x ) = x 2 et a = 1.
La tangente à f au point d’abscisse a = 1 a donc pour équation :
y = f ′(1)( x − 1) + f (1).
Nous avons donc besoin de calculer f ′(1) et f (1). On calcule f ′( x ).
On sait que f ′( x ) = 2x donc f ′(1) = 2 × 1 = 2. Comme f (1) = 11 = 1 , la tangente
T en question a donc pour équation : y = 2( x − 1) + 1 c’est-à-dire y = 2x − 1.
Ceci signifie qu’au voisinage du point de f d’abscisse 1, f et T sont presque
confondues. Dit autrement, lorsque x est proche de 1, f ( x ) ≈ 2x − 1 (c’est ce
qu’on appelle l’approximation affine de f au voisinage de 1).
Séquence 4 – MA01
9
© Cned - Académie en ligne
Puisque x = 1, 001 est proche de 1 on peut en déduire que f (1,001) ≈ 2 × 1,001− 1 ;
2
autrement dit : 1,001 ≈ 1,002.
Remarque
Dans l’exemple précédent, on peut comparer avec la valeur exacte de 1, 0012 qui
est 1, 002 001. On fait donc une erreur de 0, 000 001 (c’est-à-dire de 10
lement !) en remplaçant x
2
−6
seu-
par 2x − 1 pour x = 1, 001. Cette approximation est
d’autant meilleure que x est proche de 1.
3. Dérivation et opérations sur les fonctions
Soit u et v deux fonctions définies et dérivables sur un même intervalle I. Leurs
dérivées sont u ′ et v ′.
Fonction
Dérivée
u +v
(u + v )′ = u ′ + v ′
k u où k ∈.
(k u ) ′ = k u ′
uv
(uv )′ = u ′v + uv ′
u2
(u 2 )′ = 2 ⋅ u ⋅ u ′
u3
(u 3 )′ = 3 ⋅ u 2 ⋅ u ′
u n où n ∈ − {0 }
(u n )′ = n ⋅ u n −1 ⋅ u ′
1
(v est une fonction ne s’annulant pas sur I )
v
 1 ′ −v ′
 v  = 2
v
u
(v est une fonction ne s’annulant pas sur I )
v
 u  ′ u ′ ⋅v − u ⋅v ′
 v  =
v2
Remarque
A l’issue de cette séquence, vous pourrez enrichir ce tableau en y ajoutant la foncu
tion e (exponentielle d’une fonction). La séquence 5, permettra d’y ajouter aussi
ln(u ) (logarithme népérien d’une fonction).
Exercice
10
© Cned - Académie en ligne
Dans chaque cas, déterminer la fonction dérivée de la fonction :
Séquence 4 – MA01
a) f définie sur par f ( x ) = 3x 8 − 7x − 1.
b) g définie sur ]2 ; + ∞ [ par g ( x ) =
Solution
3
x2 − 4
.
a) f est une fonction polynôme donc elle est dérivable sur .
f est du type u + v avec u ( x ) = 3x 8 et v ( x ) = −7x − 1.
Le formulaire précédent nous indique que u ′( x ) = 3 × 8 x 7 = 24 x 7 et v ′( x ) = −7.
Comme f ′ = u ′ + v ′ , f ’(x) = 24x7 – 7 pour tout réel x.
b) g est bien définie et dérivable sur ]2 ; + ∞ [ puisque x 3 et x x 2 − 4
le sont et que x x 2 − 4 ne s’annule pas sur ]2 ; + ∞ [. De plus, g est de la forme
u
avec u ( x ) = 3 et v ( x ) = x 2 − 4.
v
On calcule u ′( x ) = 0 et v ′( x ) = 2x .
u ′v − uv ′
g′ =
on obtient
Par conséquent, avec la formule
2
2
v
0 × ( x − 4 ) − 3 × 2x
−6 x
g ′( x ) =
.
=
2
2
2
(x − 4)
( x − 4 )2
1
donc, à l’aide
Autre méthode (plus directe) : on remarque que g ( x ) = 3 × 2
x −4
 −2x 
−6 x
 1  ′ −u ′
 =
.
, on calcule : g '( x ) = 3 ×  2
de la formule   =
2
2
u
 ( x − 4)  ( x − 4)2
u2
4. Applications de la dérivation
Ici, on considère une fonction f dérivable sur un intervalle I.
Théorèmes
Logique
«
f est constante sur I »
équivaut à « pour tout réel x ∈I , f ’(x) = 0 ».
«
f est croissante sur I »
équivaut à « pour tout réel x ∈I , f ’(x) ≥ 0 ».
«
f est décroissante sur I » équivaut à « pour tout réel x ∈I , f ’(x) ≤ 0 ».
Si
f a un extremum en un point d’abscisse a alors f ′(a ) = 0.
La locution « équivaut à » signifie – pour la deuxième phrase, par exemple – que :
Si f ′( x ) ≥ 0 pour tout réel x de I alors f est croissante
et
Si f est croissante alors f ′( x ) ≥ 0 pour tout réel x de I.
Séquence 4 – MA01
11
© Cned - Académie en ligne
C’est l’implication qu’on utilise souvent dans les exercices lorsqu’on étudie le
sens de variation d’une fonction f.
Expliquons comment.
Méthode
1re étape : On dérive la fonction.
2e étape : On étudie le signe de la dérivée.
3e étape : On conclut à l’aide des théorèmes précédents.
Pour la 2e étape (la plus délicate), essentiellement trois cas peuvent se présenter :
1er cas : « le signe de f ′( x ) est évident ».
Il faut bien observer l’expression de f ′( x ) mais aussi s’habituer à
repérer un nombre qui est toujours positif (une racine carrée, un carré, l’exponentielle d’un nombre, …).
utiliser des règles simples comme « la somme de nombres positifs est positive », …
utiliser les identités remarquables.
Exercice
Solution
Soit f la fonction définie sur ] − 2; +∞ [ par f ( x ) =
x
. Etudier les variations de f.
x +2
Calcul de f ′( x ) : f est une fonction homographique (quotient de deux fonctions
affines) dont le dénominateur x + 2 ne s’annule pas sur ] − 2; +∞ [ ; donc f est
1× ( x + 2) − x × 1
2
dérivable sur ] − 2; +∞ [ et f ′( x ) =
.
=
( x + 2)2
( x + 2)2
de f ′( x ) : f ′( x ) est le quotient de 2 et de ( x + 2)2. Or, pour tout réel
x de ] − 2; +∞ [ , ( x + 2)2 > 0 (car un carré est toujours positif) et 2 > 0 ; par
conséquent, pour tout réel x > –2, f ′( x ) qui est le quotient de deux nombres
positifs est positif. En résumé : pour tout x de ]–2,+∞[ f ’(x) ≥ 0.
Signe
Application du théorème : comme f est une fonction dérivable vérifiant pour
tout x ∈] − 2; +∞ [, f ’(x) ≥ 0, d’après un théorème du cours on conclut que f est
croissante sur .
2e cas : « le signe de f ′( x ) n’est pas évident mais on peut transformer l’écriture
de f ′( x ) ».
Pour étudier le signe de f ′( x ) , on peut factoriser ou regrouper au même dénominateur. Ensuite, on s’aide d’un tableau de signes.
Exercice
Soit g la fonction définie sur par g ( x ) = 4 x 3 + 6 x 2. Etudier les variations
de g .
Solution
Calcul de g ′( x ) : g est une fonction polynôme donc g est dérivable sur et
g ′( x ) = 12x 2 + 12x .
12
© Cned - Académie en ligne
Séquence 4 – MA01
Signe de g ′( x ) : g ′( x ) est la somme de 12x 2 qui est positif (c’est un carré)
lorsque x parcourt et de 12x qui n’est pas de signe constant lorsque x parcourt
. On ne peut donc rien conclure sur le signe de la somme. On cherche à transformer 12x 2 + 12x . Ici, on peut factoriser g ′( x ) pour l’écrire : g ′( x ) = 12x ( x + 1).
Sous cette forme, g ′( x ) est le produit de 12x et de x + 1 dont on connait parfaitement le signe lorsque x parcourt (ce sont des fonctions affines).
On utilise un tableau de signes :
−∞
x
0
–1
12x
–
–
x+1
–
0
+
12x (x + 1)
+
0
–
0
+∞
+
+
0
+
g (x)
Pour
remplir la dernière ligne du tableau précédent, nous avons appliqué trois
fois les théorèmes du cours (3e étape décrite ci-dessus) sur chacun des trois
intervalles ] − ∞; − 1[ , ] − 1; 0[ et ]0 ; + ∞ [.
3e cas :« le signe de f ′( x ) n’est pas évident et on ne peut pas transformer
l’écriture de f ′( x ) ».
On peut alors essayer de résoudre l’inéquation f ( x ) ≥ 0 en s’aidant des variations des fonctions usuelles.
Exercice
Solution
1
Étudier les variations de la fonction h définie sur par h ( x ) = x 4 − 8 x + 1.
4
Calcul
de h ′( x ) : h est une fonction polynôme donc h est dérivable sur et
h ′( x ) = x 3 − 8.
de h ′( x ) : h ′( x ) n’a pas un signe constant lorsque x parcourt et
il n’apparait pas non plus de factorisation simple. On peut alors penser à résoudre h ′( x ) ≥ 0.
Signe
h ′( x ) ≥ 0 ⇔
x3 −8 ≥ 0
⇔
x3 ≥ 8
⇔
x 3 ≥ 23
Comme la fonction cube est croissante, elle ne change pas l’ordre donc
x 3 ≥ 23 ⇔ x ≥ 2
Des équivalences qui précèdent, on retient : h ′( x ) ≥ 0 ⇔ x ≥ 2 , autrement dit,
h ′( x ) ≥ 0 ⇔ x ∈[2 ; + ∞ [.
Séquence 4 – MA01
13
© Cned - Académie en ligne
On
conclut à l’aide du théorème du cours que h est croissante sur l’intervalle
[2 ; + ∞ [.
En reprenant le point précédent et en résolvant l’inéquation h ′( x ) ≤ 0 (les calculs
sont analogues) on conclut que h est décroissante sur l’intervalle ] − ∞ ; 2]. D’où
le tableau de variations :
x
h ′( x )
h( x )
14
© Cned - Académie en ligne
Séquence 4 – MA01
−∞
+∞
2
–
0
+
2
A
Introduction aux
fonctions exponentielles
Objectifs du chapitre
Une suite (un ) peut être vue comme une “fonction” n un qui n’est définie
que pour les entiers n. Nous allons voir dans ce chapitre comment prolonger
cette “fonction” pour des valeurs x réelles et ainsi former une vraie fonction
x f ( x ). Les suites qui nous intéressent sont les suites géométriques de premier terme 1 et de raison q strictement positive. Vous comprendrez à l’activité 2
pourquoi elles sont si intéressantes …
B
Activité 1
Pour débuter
La moyenne d’accord, mais laquelle ?
Céleste a été absente ce trimestre et n’a que deux notes en SVT ; 15 et 5. Pour
calculer sa moyenne trimestrielle le professeur de SVT – qui est un peu joueur –
lui propose le choix suivant : soit il prend la moyenne arithmétique de 5 et 15,
soit il prend la moyenne géométrique de 5 et 15.
Comment se calcule la moyenne arithmétique ? la moyenne géométrique ?
(vous pouvez vous aider d’un dictionnaire ou d’Internet pour chercher le sens des
mots inconnus)
Quel choix est le plus avantageux pour Céleste ?
Au trimestre suivant, le professeur de mathématiques – qui est un peu étourdi
– n’a donné que deux devoirs aux élèves. Il propose à chaque élève de la classe
de choisir entre la moyenne arithmétique et la moyenne géométrique des notes
qu’il a obtenues.
Pour chaque élève, quel choix est le plus avantageux ?
Activité 2
Propriétés des suites géométriques de premier terme 1 et de raison
q strictement positive
Représentation graphique de la suite (u )
n
Ici q = 2.
Séquence 4 – MA01
15
© Cned - Académie en ligne
Compléter le tableau de valeurs suivant et placer les points obtenus sur le graphique.
n
un
0
1
2
3
1
0
1
Propriétés de la suite (u )
n
Ici encore q = 2.
a) Compléter le tableau précédent pour n ∈{ 4; 5; 6; 7} .
Calculer u1+ 2 (attention, ce n’est pas la même chose que u1 + 2 ) puis u1 × u 2 .
b) Calculer u 3+ 4 puis u 3 × u 4 . Qu’observez-vous ? Expliquer à l’aide de l’égalité un = 2n ; puis généraliser ce résultat en complétant l’égalité um + n = ...
c) La suite (un ) est en fait une fonction f définie de dans par f (n ) = un = 2n .
Ainsi, on peut noter f : → .
n un
Réécrire le résultat obtenu au b) à l’aide de la fonction f.
Interprétation géométrique
Désormais q est un nombre réel strictement positif quelconque.
On souhaite interpréter graphiquement l’égalité précédente. Pour cela, on
fixe arbitrairement un nombre n ∈∗. On considère les trois points consécutifs A, B, C du nuage représentant la suite (un ) dont les coordonnées sont :
A(n − 1 ; un −1), B(n ; un ) et C(n + 1 ; un +1).
16
© Cned - Académie en ligne
Séquence 4 – MA01
A l’aide du schéma suivant, compléter les phrases :
C
un+1
⫻q
⫻q
B
un
un–1
A
O
n–1
n
n+1
L’ordonnée
du point C est égale à ………… l’ordonnée du point B.
La moyenne arithmétique des abscisses des points A et C est égale à …………
du point …
La moyenne géométrique des ordonnées des points A et C est égale à …………
du point …
Remarque
Au cours de l’activité 2, nous avons vu que la suite géométrique de raison 2 et de
n
premier terme 1, autrement dit, la suite de terme général un = 2 peut être vue
comme une fonction f : → vérifiant
Pour tous entiers n et m de , f (n + m ) = f (n ) × f (m ) (on dit que f transforme une somme en un produit). Cette égalité qui traduit simplement que
2n + m = 2n × 2m est encore valable dans le cas plus général d’une suite géomén +m
= qn × qm.
trique dont la raison serait un nombre q > 0 puisque q
Dans la suite, on considère donc la
Remarque
fonction f définie par f (n ) = q n où
Remarquons aussi que, puisque
q > 0 est un nombre réel fixé.
q > 0, on a aussi pour tout entier
n de , f (n ) > 0.
L’objectif de l’activité 3 est d’étendre
cette fonction f à en complétant le
nuage de points de sorte que les propriétés en évidence ci-dessus soient conservées.
Activité 3
Prolongement à 1
1
On connaît les puissances négatives de q. Ainsi q −1 =
; q −2 =
; …;
q
q2
1
−n
q =
…
qn
On peut prolonger f à en posant f ( p ) = q p pour tout p de .
Séquence 4 – MA01
17
© Cned - Académie en ligne
Pour cette question, q = 2.
a) Compléter le tableau de valeurs suivant puis placer les points obtenus sur le
graphique.
p up = f(p)
–3
–2
–1
0
1
2
3
M3
M2
M1
M0
b) Calculer f ( −2) × f ( −1) puis f ( −2 − 1).
c) Calculer f ( 3) × f ( −2) puis f ( 3 − 2). Que remarque-t-on ?
d) Donner un autre exemple de cette propriété.
Pour cette question, on revient à q > 0.
Justifier que :
Pour
tous entiers relatifs m et n, on a f (m + n ) = f (m ) × f (n ).
f est strictement positive ; autrement dit, pour tout entier relatif p , f (p) > 0.
L’objectif de l’activité 4 est d’étendre cette fonction f à , en complétant le
nuage de points de sorte que les deux propriétés précédentes soient conservées.
Activité 4
Prolongement à Le principe : entre deux points du nuage précédent, on ajoute un nouveau point
ayant pour abscisse la moyenne arithmétique des abscisses de ces deux points
et pour ordonnée la moyenne géométrique de leurs ordonnées. Et on réitère le
procédé. Il s’agit d’un processus dichotomique.
Reprenons l’exemple précédent : q = 2.
18
© Cned - Académie en ligne
Séquence 4 – MA01
Première étape
Compléter le tableau suivant puis le nuage de points en respectant le principe
énoncé dans l’activité 3.
moyenne arithmétique
Exemple
1

Entre M0 ( 0 ; 1) et M1(1 ; 2) on va ajouter le point M 1  ; 2  puisque
2

2
moyenne géométrique
0 +1
2
Point
abscisse
=
1
2
et
1× 2 = 2 .
M −3
M −2
M −1
M0
–3
–2
–1
0
M1
2
1
M1
M2
M3
1
2
3
2
4
8
2
ordon- 1
née 8 = 0 , 125
1
4
1
= 0 , 25
2
1
= 0, 5
2 ≈1, 4
Pour l’ordonnée, donner la valeur exacte, puis une valeur approchée, si nécessaire.
M3
M2
M1
M–3 M–2
M0
M–1
O
La fonction f :
0,5 ; 1 ; 1,5 ; …
R→
p 2p
1
est alors définie en … ; –3 ; –2,5 ; – 2 ; – 1,5 ; – 1 ; – 0,5 ; 0 ;
Autrement dit, f est définie pour tous les réels du type
m
avec m ∈.
2
Séquence 4 – MA01
19
© Cned - Académie en ligne
Le tableau précédent peut ainsi s’écrire :
abscisse
m
−3 =
−6
2
−2, 5 =
−5
2
−2 =
−4
−3
−1, 5 =
2
2
−2
−1 =
2
−0 , 5 = −
1
2
0=
0
0, 5 =
2
1
1=
2
2
2
1, 5 =
3
2=
2
4
2
2, 5 =
5
2
3=
6
2
2
ordonnée
 m
f
 2
1
1
1
8
32
4
1
1
1
2
8
1
2
2
4
8
8
32
2
Nous allons maintenant écrire différemment les nombres du tableau précédent…
pour y voir plus clair.
Calculer
( 2)
5
puis
( 2)
−5
.
Compléter ensuite le tableau
Abscisse
m
2
…
…
…
…
…
…
…
…
…
…
…
…
…
2
2
2
2
2
2
2
2
2
2
2
2
2
Ordonnée
 m
 2 
f
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
…
2
× 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Dans le cas présent (où q = 2), à la lecture de la 2e ligne du tableau précédent,
une règle semble se dégager. Compléter l’égalité suivante résumant cette règle :
f (...) = (...) .
...
Placer le point M 5 dont l’abscisse est la moyenne (arithmétique) des abscisses
2
des points M2 et M 3 .
Ce point est-il situé au-dessus ou au-dessous du milieu du segment [M2M 3 ] ?
Deuxième étape
Nous poursuivons avec l’exemple précédent : q = 2. Nous sommes partis de la
fonction f : p 2p bien connue lorsque p est un entier ; nous l’avons étendue
aux entiers relatifs et nous venons de l’étendre aux moitiés d’entiers relatifs.
Nous allons maintenant l’étendre aux moitiés de ces derniers, c’est-à-dire, aux
m
nombres x qui sont le quart d’un entier relatif ; autrement dit, de la forme x =
4
où m ∈. Nous réitérons pour cela le processus de dichotomie. Comme précédemment, donnons d’abord un exemple.
20
© Cned - Académie en ligne
Séquence 4 – MA01
moyenne arithmétique
Exemple
1
1

Entre M0 (0 ; 1) et M 1  ; 2  , on va ajouter le point M 1  ;
2

4
2
4

2  puisque

moyenne géométrique
1
2 = 1 et 1× 2 =
2.
2
4
Compléter le tableau suivant puis placer les nouveaux points du nuage (sans leur
nom pour éviter la surcharge) sur le graphique précédent.
0+
M −3
Point
–3
abscisse
M 11 M 5
−
−
−
4
11
4
−
2
5
−
2
M
M −2
9
−
−
–2
4
7
−
4
2
M −1
3
–1
2
0,35
ordonnée
Point
3
M1
M1
4
2
abscisse
ordonnée
C
M3
M1
1
1
3
4
2
4
0,5
M2
2
M 1
−
−
2
1
M0
0
2
0,71
1
M3
1,19
Cours
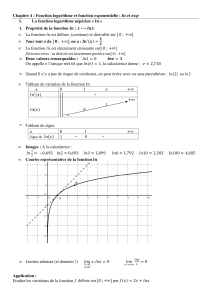
1. Prolongement des suites géométriques,
définition de x q x avec q > 0.
Au cours des activités 2, 3 et 4 nous avons progressivement étendu la fonction
x 2x pour des valeurs de x égales au quart d’un nombre entier. Ainsi, par
1
3
3
2 et 2 4 =  2  .


Le principe utilisé dans le processus dichotomique consistant, à partir de deux
points déjà construits, d’en construire un nouveau dont l’abscisse est la moyenne
arithmétique des abscisses des deux points de départ et l’ordonnée, la moyenne
géométrique de leurs ordonnées repose sur les deux propriétés suivantes imposées au départ :
exemple 2 4 =
Séquence 4 – MA01
21
© Cned - Académie en ligne
La fonction f qui prolonge la fonction x 2x doit
rester
strictement positive
transformer chaque somme en un produit.
En itérant le processus décrit, on obtient un nombre croissant de points suggérant la courbe d’une fonction.
1
O
1
On admet que cette fonction existe, est unique et qu’elle est dérivable sur .
Définition
Il existe une unique fonction f dérivable sur , strictement positive, transformant chaque somme en un produit et égale à 2n en chaque x = n entier. C’est la fonction exponentielle de base 2.
22
© Cned - Académie en ligne
Séquence 4 – MA01
Voici la courbe (c’est-à-dire, le tracé continu) de la fonction exponentielle de
base 2.
1
O
1
Ne pas confondre la « fonction exponentielle de base 2 » avec la « fonction carré ».
2
La fonction carré est donnée par g ( x ) = x . Elle ne transforme pas chaque somme
en produit puisqu’en général on n’a pas ( x + y )2 = x 2 y 2 ; il suffit de vérifier, par
2
2
2
exemple, que (1+ 2) = 9 et 1 × 2 = 4 mais 9 ≠ 4. En général, g ( x + y ) est
différent de g ( x ) × g ( y ) .
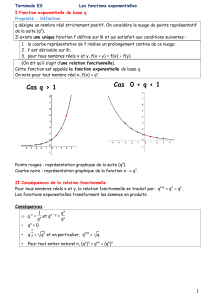
La définition se généralise à tout réel q > 0. On obtient ainsi la fonction exponentielle de base q.
Définition
Soit q un réel strictement positif fixé.
Il existe une unique fonction f dérivable sur , strictement positive, transformant chaque somme en un produit et égale à q n en chaque x = n
entier. C’est la fonction exponentielle de base q.
A l’aide de votre calculatrice, vous pouvez obtenir les courbes des fonctions
x q x pour différentes valeurs q. Voici deux exemples :
Séquence 4 – MA01
23
© Cned - Académie en ligne
Autres exemples
nuage de points avec q = 0,5
nuage de points avec q = 1,5
courbe de la fonction exponentielle de base 0,5 :
courbe de la fonction exponentielle de base 1,5 :
1
O
1
1
O
1
Les fonctions exponentielles x q x vérifient toutes f (0 ) = 1 (on calcule
f (0 ) = q 0 = 1 ) puisqu’elles prolongent les suites géométriques (un ) de premier
terme u 0 = 1 .
2. Fonctions exponentielles de base q > 0
a) Notation puissance
Soit f la fonction exponentielle de base q > 0.
On a f (n ) = q n pour tout n ∈.
On étend cette notation à en posant f ( x ) = q x pour tout réel x.
24
© Cned - Académie en ligne
Séquence 4 – MA01
Notation
La fonction exponentielle de base q est alors la fonction f définie sur
par f ( x ) = q x .
Remarques
Le
fait que f transforme chaque somme en produit, c’est-à-dire
f ( x + y ) = f ( x ) × f ( y ) pour tous réels x et
y, s’écrit simplement :
x +y
x
y
q
= q × q ce qui justifie l’emploi de cette notation puisqu’on retrouve une
propriété des puissances entières.
La règle dégagée des observations de la question de l’activité 4, s’écrit
 m
f =
 2
( q)
m
pour tout m ∈.
m
Avec la notation puissance, cette règle s’écrit q 2 =
m = 1 , on obtient
1
q2
( q)
m
. En particulier, pour
= q , ce qu’on peut constater avec la calculatrice en com1
parant, par exemple, les valeurs obtenues pour
3 et pour 3 2 . Pour obtenir cette
dernière, on peut entrer 3 ^ ( 1 ÷ 2 )
Nous admettrons que la fonction f ainsi construite est continue sur
(on trace
sa courbe sans lever le crayon).
b) Propriétés
Soit q un réel strictement positif.
La fonction exponentielle de base q est le prolongement continu de la suite géométrique (un ) de premier terme u 0 = 1 et de raison q (le terme général de cette
suite est un = q n ) .
En notant f cette fonction, on écrit : f :
Propriété 1 (admis)
Les fonctions exponentielles sont :
strictement
positives sur .
continues
sur .
dérivables
sur .
→
x qx
Propriété 2
Les fonctions exponentielles x q x
transforment
chaque somme en un produit :
pour tous réels x et y, f ( x + y ) = f ( x ) × f ( y )
ce qu’on peut donc écrire q x + y = q x × q y .
1
: pour tout réel x, q − x =
qx
qx
vérifient : pour tous réels x et y,
= q x −y .
y
q
vérifient
Séquence 4 – MA01
25
© Cned - Académie en ligne
Démonstration
La propriété résulte d’un choix fait au départ, lors de la construction des fonctions exponentielles.
L’existence de fonctions (les fonctions exponentielles) vérifiant cette propriété est
admise, conformément au programme.
La propriété découle de la propriété ). En effet, il suffit de choisir y = − x
dans la propriété
pour obtenir q x − x = q x × q − x soit q 0 = q x × q − x d’où
1= q x × q − x soit finalement la propriété en divisant par q x .
La propriété découle des propriétés et .
Remarque
( )
On admet aussi : pour tous réels x et y, q x
y
= q xy .
Par conséquent, les fonctions exponentielles vérifient toutes les propriétés
opératoires des puissances entières que vous connaissez depuis le collège.
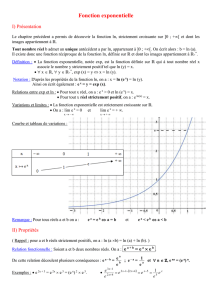
Propriété 3
Lorsque 0 < q < 1 , la fonction exponentielle de base q, x q x est strictement décroissante sur .
x
−∞
+∞
1
qx
1
O
Lorsque q > 1, la fonction exponentielle de base q, x q x est strictement
croissante sur .
x
−∞
qx
+∞
1
O
1
Lorsque q = 1, la fonction exponentielle de base q, x q x est constante,
égale à 1, sur .
Remarque
R
Ces résultats prolongent les résultats déjà vus sur le sens de variation des suites
géométriques étudiées en classe de première.
26
© Cned - Académie en ligne
Séquence 4 – MA01
D
Exercice 1
Exercices d’apprentissage
Simplifier les expressions suivantes (les écrire sous la forme a b ou a b c d , avec
a ≠c ) :
b) 0, 4 3 × 0, 4 −2,5
a) 23,7 × 25
c)
3, 9 × 3, 9−2 d)
3−8,1 × 22
2
3
× 2−2,1
Exercice 2
Déterminer la fonction exponentielle f telle que f (2) = 1, 2.
Exercice 3
Représenter sur un même graphique (unités : 1cm sur (Ox) et 2cm sur (Oy )) dans
un repère (O ,I , J )
Exercice 4
la
fonction exponentielle de base 0,8.
la
fonction puissance −0, 8; c’est-à-dire x x −0,8 sur l’intervalle [0 ; 15] .
Résoudre dans les équations suivantes :
a) x 3 = 1
b) x 3 = 2
c) x 3 = −8
d) x 3 = −5
Déterminer le réel strictement positif x tel que x −1,5 = 2.
Exercice 5
Une seule des quatre courbes suivantes ne représente pas une fonction exponentielle, laquelle ?
Les trois autres courbes représentent les fonctions exponentielles de bases
2, 5 ;
2
et 3.
3
A vous d’attribuer chaque courbe à sa fonction (sans la calculatrice !).
(1)
1
1
(2)
O
1
O
1
Séquence 4 – MA01
27
© Cned - Académie en ligne
(4)
(3)
1
1
O
28
© Cned - Académie en ligne
Séquence 4 – MA01
1
O
1
3
A
La fonction exponentielle
de base e
Objectifs du chapitre
Parmi les fonctions exponentielles x q x définies pour toutes les valeurs de
q > 0 au chapitre 2, l’une d’entre elles est particulièrement intéressante. Nous
allons découvrir laquelle…
B
Activité 5
Pour débuter
Laquelle choisir ?
Les courbes des fonctions exponentielles passent toutes par un même point A.
Quelles sont les coordonnées de A ?
Déterminer l’équation de la droite de pente 1 passant par A.
A l’aide du logiciel Geogebra :
a)
définir un nombre q qu’on pourra piloter à l’aide d’un curseur. On choisira un
curseur de largeur 500 dont on fixera les propriétés afin que le nombre q varie
dans l’intervalle ]0 ; 5] avec un incrément de 0,001.
tracer
la droite tracer la courbe de la fonction exponentielle de base q (on appelle f cette
fonction) puis sa tangente au point d’abscisse zéro (vous pouvez entrer au clavier
Tangente[0, f] dans le champ de saisie)
b) Faites varier q, à l’aide du curseur. Pour quelle(s) valeur(s) de q la droite et
la tangente coïncident-elles ?
c) Que vaut alors f ′(0 ) ?
d) Modifier les propriétés du curseur pour que le nombre q puisse prendre des valeurs dans l’intervalle [0 ; 30]. Compléter ensuite le tableau suivant (les valeurs
seront arrondies à la 2e décimale) :
Séquence 4 – MA01
29
© Cned - Académie en ligne
f ′(0 )
1
q
0,1 0,5 0,9 1,3 1,5 1,8
2
2,2 2,3 2,4 2,5 2,6 2,7
2,8 2,9
3
4,5 7,5
e) Compléter la phrase « La fonction exponentielle f de base q ≈ .............. vérifie
f ′(0 ) = ....... ».
C
Cours
1. Définition de la fonction exponentielle de
base e
Théorème
Il existe une unique fonction exponentielle f telle que f ′(0 ) = 1.
Cette fonction est appelée fonction exponentielle de base e et est notée exp.
Avec la notation puissance, exp(x) = e x pour tout réel x.
Remarque
Conformément au programme, ce résultat est admis.
La base q de cette fonction exponentielle exp est un nombre réel noté
e environ égal à 2,7 – comme nous avons pu le voir dans l’activité 5 –.
En mathématiques, ce nombre joue un rôle presque aussi important que
le nombre π . Comme exp(1) = e1 = e , le nombre e est l’image de 1 par la
fonction exp.
Avec la Texas-Instruments TI82, la fonction exp s’obtient de la façon
suivante :
Et avec la Casio Graph25, de la façon suivante :
Vous pouvez ainsi obtenir les premières décimales du nombre e :
e ≈ 2, 71828182846 .
D’après le chapitre 2, la fonction exponentielle de base e est le prolonge-
ment de la suite géométrique de premier terme u 0 = 1 et de raison e. Pour
cette raison (sans jeu de mot !), on a en particulier pour tout entier n ∈ ,
exp(n ) = en = e
×
e
×
e ×
... ×e et aussi e0 = 1 .
n fois e
30
© Cned - Académie en ligne
Séquence 4 – MA01
2. Propriétés de la fonction exponentielle de
base e
La fonction exp est une fonction exponentielle. Elle vérifie donc les propriétés de
ces dernières, étudiées au chapitre 2. Rappelons-les :
Propriété analytiques
La fonction exp est :
définie
sur continue
sur dérivable
sur strictement
positive sur le
nombre dérivé de la fonction exp en 0 est égal à 1 : exp ′(0 ) = 1.
La 4e propriété implique en particulier que l’exponentielle de n’importe quel
réel est strictement positive donc jamais nulle.
La 5e propriété est propre à la fonction exponentielle de base e, et à elle
seule.
Propriétés algébriques
La
fonction exp transforme chaque somme en un produit,
autrement dit : exp( x + y ) = exp( x ) × exp( y ) pour tous réels x et y.
On a aussi :
1
pour tout réel x (l’exponentielle de l’opposé est l’inexp( x )
verse de l’exponentielle).
exp( − x ) =
exp( x )
pour tous réels x et y (la fonction exp transforme une
exp(
y
)
différence
en un quotient).
exp( x − y ) =
Ces propriétés légitiment l’utilisation de la notation puissance ce qui rend
leur utilisation plus naturelle : pour tous réels x et y, e x + y = e x × e y ;
y
ex
1
e− x =
; e x = e xy .
; ex − y =
ex
ey
( )
Remarque
L’égalité e x + y = e x × e y vraie pour tous réels x et y s’appelle la relation
fonctionnelle des fonctions exponentielles: c’est d’elle dont nous sommes
partis (écrite sous la forme f ( x + y ) = f ( x ) × f ( y ) ) pour construire les fonctions exponentielles. Il faut savoir appliquer cette relation dans les deux
sens. Par exemple, e x × e y = e x + y .
Séquence 4 – MA01
31
© Cned - Académie en ligne
D
Exercice 6
Exercices d’apprentissage
Simplifier les expressions
2
A = e ×e
D=
Exercice 7
ex
e
−2x
−1,5
× e
× e2
;
B=
;
e −1 × e5,5
e × e 0 ,8
E = e x × (e − x − 1).
Montrer que pour tout réel x :
a) (e x + e − x )2 − (e x − e − x )2 = 4.
b)
32
© Cned - Académie en ligne
ex
x
e +e
Séquence 4 – MA01
−x
=
1
1+ e −2x
.
;
 1
C = 
 e3 
2
;
4
A
Dérivation et fonction
exponentielle (base e)
Objectifs du chapitre
Parmi les fonctions exponentielles x q x définies pour toutes les valeurs de
q > 0 au chapitre 2, l’une d’entre elles est particulièrement intéressante : il s’agit
de la fonction exponentielle de base e. Nous allons maintenant découvrir pourquoi…
B
Activité 6
Pour débuter
Le clone de sa dérivée
Faites varier q et déterminez la valeur de q pour laquelle les deux courbes se
superposent.
Que ceci signifie pour exp ′( x ) ?
Activité 7
Stoïque par dérivation
Cette activité est difficile et peut être omise en première étude.
A l’aide de la définition du nombre dérivé exp ′(0 ) montrer que lim
h →0
En déduire que exp ′(0 ) = exp(0 ).
eh − 1
= 1.
h
A l’aide de la relation fonctionnelle des fonctions exponentielles, factoriser
l’expression suivante :
e 4 ,7+ h − e 4 ,7 . En déduire que exp ′( 4 , 7) = exp( 4 , 7).
Proposer une généralisation du résultat précédent pour un réel a quelconque.
Activité 8
Comportements asymptotiques (limites)
a) Quelle est la nature de la suite ( en ) ? En déduire
lim en .
n →+∞
b) Pour tout n ∈, on note An le point d’abscisse n de la courbe de la fonction
exponentielle.
Séquence 4 – MA01
33
© Cned - Académie en ligne
Déterminer les coordonnées de A100 puis celles de A200. Avec le logiciel Geogebra, tracer la courbe de la fonction exponentielle puis observer la position du
point An lorsque n prend de grandes valeurs. Interpréter.
a) Quelle est la nature de la suite (e −n ) ? En déduire lim e −n .
n →+∞
b) Pour tout n ∈, on note Bn le point d’abscisse −n de la courbe de la fonction exponentielle.
Déterminer les coordonnées de B100 puis celles de B200. Avec le logiciel Geogebra, tracer la courbe de la fonction exponentielle puis observer la position du
point Bn lorsque n prend de grandes valeurs. Interpréter.
C
Cours
Quand on parle de la fonction exponentielle, ceci sous-entend la fonction exponentielle de base e, c’est-à-dire exp.
→
exp :
x ex
L’ensemble de définition de la fonction exponentielle est .
1. Fonction dérivée de la fonction exponentielle
Théorème 1
La fonction exp est dérivable sur et la fonction dérivée de exp est ellemême.
Autrement dit, exp ′( x ) = exp( x ) = e x pour tout réel x.
Démonstration
Rappelons brièvement les ingrédients de la démonstration (vue à l’activité 7) de
l’égalité exp ′( x ) = exp( x ) :
On part de la définition du nombre dérivé
ea + h − ea
exp ′(a ) = lim
h
h →0
34
© Cned - Académie en ligne
Séquence 4 – MA01
D’après la relation fonctionnelle des fonctions exponentielles ea + h = ea × eh
On peut donc factoriser le numérateur :
ea (eh − 1)
h
h →0
exp ′(a ) = lim
Comme ea ne dépend pas de h :
eh − 1
h →0 h
exp ′(a ) = ea × lim
Comme
e0 = 1 , ceci nous rappelle la définition du nombre dérivé
e0 + h − e0
, d’où :
h
h →0
exp ′(0 ) = lim
exp ′(a ) = ea × exp ′(0 )
Mais, la base e a été précisément choisie parmi les bases q des fonctions exponentielles pour que :
exp ′(0 ) = 1
Conclusion : exp ′(a ) = ea (et bien sûr, le réel a qui est quelconque peut s’appeler x).
Remarque
Une fonction construite au départ pour transformer chaque somme en
produit vérifie la propriété remarquable d’être égale à sa dérivée. Méditez,
savourez…
Comme nous l’avons observé à l’activité 7 lorsqu’on cherchait à superposer la courbe de la fonction exponentielle (de base q) x q x , parmi les
fonctions exponentielles, la fonction exponentielle de base e est la seule
égale à sa dérivée (en fait, à un multiple près, c’est la seule parmi les fonctions dérivables ; mais ce résultat est hors-programme).
2. Sens de variation de la fonction exponentielle
Théorème 2
La fonction exponentielle de base e est strictement croissante.
Séquence 4 – MA01
35
© Cned - Académie en ligne
Remarque
Comme nous l’avons déjà observé, toutes les fonctions exponentielles de base q
avec q > 1 sont strictement croissantes, c’est aussi le cas de la fonction exponentielle de base e puisque e ≈ 2,7 . On se propose de démontrer ce résultat.
Démonstration
On sait que
la
fonction exponentielle est dérivable sur ,
exp ′ = exp
la
fonction exponentielle est strictement positive sur Par conséquent, le dérivée de la fonction exponentielle est strictement positive
sur Donc la fonction exponentielle est strictement croissante sur .
Ce théorème a des propriétés corollaires utiles dans la pratique.
Remarque
x
−∞
0
+∞
1
e
exp(x )
1
Nous avons déjà observé
que e > 1 ; la deuxième
ligne du tableau en apporte
la preuve.
3. Limites
Reparlons un moment de suites, plus particulièrement de limites de suites géométriques :
Comme
e > 1 , lim en = +∞ puisque la suite (en ) est une suite géométrique
n →+∞
de raison e strictement supérieure à 1.
n
n
 1
1
1
−
n
−
Comme
= lim   = 0 puisque la suite
< 1 , lim e = lim e
e
n →+∞
n →+∞
n →+∞  e 
1
(e −n ) est une suite géométrique de raison e −1 = strictement positive et strice
tement inférieure à 1.
( )
Comme nous l’avons observé à l’activité 8, ces deux résultats ont une incidence
sur la courbe de la fonction exponentielle : elle s’écrase très rapidement sur l’axe
des abscisses lorsque les abscisses (négatives) diminuent et elle croît très rapidement lorsque les abscisses (positives) augmentent. C’est pour ces raisons que,
dans la vie courante, on qualifie d’exponentielle une évolution très rapide.
36
© Cned - Académie en ligne
Séquence 4 – MA01
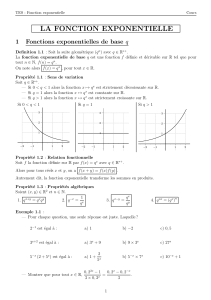
4. Courbe
Les résultats énoncés précédemment nous permettent de tracer la courbe représentative de la fonction exponentielle :
9
8
y = ex
7
6
5
4
3
2
1
O
–4
–3
–2
–1
O
1
2
3
5. Dérivée de x eu ( x )
Théorème 3
Soit u une fonction dérivable sur un intervalle I.
La fonction f définie sur I par f ( x ) = exp(u ( x )) = eu ( x ) est alors dérivable sur
I et pour tout x de I, on a : f ′( x ) = u ′( x )eu ( x ) .
Remarque
En abrégé, on retient : (eu )′ = u ′eu
Séquence 4 – MA01
37
© Cned - Académie en ligne
Exemples
Dériver les fonctions suivantes définies sur par :
a) f ( x ) = e x + 7
Solution
b) g ( x ) = e0,6 x
a) On a : f ( x ) = eu ( x ) avec u ( x ) = x + 7.
u qui est une fonction affine est dérivable sur et u ′( x ) = 1.
Le théorème 3 s’applique : f est donc une fonction dérivable sur et
f ′( x ) = u ′( x )eu ( x ) = 1× e x + 7 = f ( x ), pour tout réel x.
Remarque
Notez
qu’on peut écrire f ( x ) = e7e x = k × e x où k = e7 ; puis utiliser la
linéarité de l’opération de dérivation (vue en classe de première) pour écrire
(k × exp)′ = k × exp ′ On retrouve ainsi le (même !) résultat.
Voici un exemple de fonction différente de la fonction exponentielle (mais pas très
loin puisque la fonction f est un multiple de la fonction exponentielle) vérifiant aussi
f ′( x ) = f ( x ).
b) On a : g ( x ) = eu ( x ) avec u ( x ) = 0, 6 x .
u qui est une fonction linéaire est dérivable sur et u ′( x ) = 0, 6.
Le théorème 3 s’applique : g est donc une fonction dérivable sur et
g '( x ) = u ′( x )eu ( x ) = 0, 6 × e0,6 x , pour tout réel x.
D
Exercices d’apprentissage
Exercice 8
Déterminer une équation de la tangente (T) à la courbe de la fonction exponentielle au point d’abscisse 1. Par quel point particulier passe-t-elle ?
Exercice 9
Résoudre dans les équations suivantes :
38
© Cned - Académie en ligne
( )
ex
2
a) e 3x +1 = e x
2
b) e x =
2
1
c) e x =
ex
d) e2x − 2e x + 1 = 0.
Séquence 4 – MA01
e
2
2
(remarque : e x = e( x ) )
e)
e x = e − x +1
Exercice 10
Résoudre dans les inéquations suivantes :
a) e5x + 2 ≤ e7x − 4
d) e x + e − x > 2.
Exercice 11
3
c) e2x − e1+ x < 0
Dériver les fonctions suivantes définies sur par :
a) h ( x ) = e
Exercice 12
( ) − e1 ≥ 0
b) e x
x2 + 1x −3
2
3
2
b) k ( x ) = e7x + 5x − 3x .
Dériver les fonctions suivantes définies sur ]0 ; + ∞ [ par :
a) f ( x ) = e x
1
b) g ( x ) = e x
c) h ( x ) = e −9 x
2
−3x + 2
d) (à l’aide du logiciel XCAS) k ( x ) = e 7x + 5
Exercice 13
On considère la fonction f définie sur par f ( x ) = e x + x .
Déterminer la fonction dérivée de f.
Etudier le sens de variations de f.
Exercice 14
Etudier le sens de variations de la fonction f définie sur par f ( x ) = xe x .
Exercice 15
Dresser le tableau de variations de la fonction f définie sur par
f (x ) =
20 x
e 3x
− 1.
Tracer la courbe de la fonction f à l’aide du logiciel Geogebra.
La courbe de f coupe l’axe des abscisses en deux points d’abscisse
x 1 et x 2 avec x 1 < x 2.
Par lecture graphique, donner une valeur approchée à 10−1 de x 2.
Calculer f (1) puis, à l’aide du tableau de variations de f, en déduire la position
de x 2 par rapport à 1.
Exercice 16
(d’après bac ES – Polynésie – juin 2011)
Soit f une fonction définie sur l’ensemble ] − ∞ ; 1[∪]1 ; + ∞ [.
On note f la courbe représentative de f dans le plan muni d’un repère orthonormé.
On suppose que f est dérivable sur chacun des intervalles ] − ∞ ; 1[ et ]1 ; + ∞ [
et on note f ′ la fonction dérivée de f. On suppose aussi que f admet le tableau
de variation suivant :
Séquence 4 – MA01
39
© Cned - Académie en ligne
x
−∞
1
6
+∞
2
+∞
+∞
f
−∞
3
Pour chacune des quatre affirmations ci-dessous, une seule de ces trois propositions convient :
➟ Vraie
ou
➟ Fausse
ou ➟ Les informations données ne permettent pas de conclure.
Recopier sur la copie le numéro de la question et la proposition choisie. Justifier
votre réponse.
L’équation f ( x ) = 0 admet une unique solution sur ] − ∞ ; 1[∪]1 ; + ∞ [.
Pour tout réel x appartenant à l’intervalle ]1 ; + ∞ [, f ‘ (x ) ≥ 0.
Soit g la fonction définie sur ] − ∞ ; 1 [∪] 1 ; + ∞ [ par g ( x ) = ef ( x ) .
g (6) = e3 .
g ′( 3) ≥ 0.
40
© Cned - Académie en ligne
Séquence 4 – MA01
5
Synthèse
de la séquence
1. Rappel de dérivation
Graphiquement, f est dérivable en a si la courbe de f admet au point d’abscisse a
une tangente (T) non parallèle à l’axe des ordonnées : f ’(a) est alors le coefficient
directeur (ou la pente) de cette tangente. Par conséquent, (T) a pour équation :
y = f ′(a )( x − a ) + f (a ).
2. Les fonctions exponentielles
Soit q > 0. La fonction exponentielle de base q est la fonction f définie sur par f ( x ) = q x .
C’est le prolongement continu de la suite géométrique (un ) de premier terme
u0 = 1 et de raison q.
Propriété
Les
fonctions exponentielles sont strictement positives sur (donc jamais nulles).
Les
fonctions exponentielles sont continues et dérivables sur .
tous réels x et y, on a : q x + y = q x × q y (transformation de chaque
somme en produit).
Pour
q
−x
=
1
q
x
;
qx
q
y
= q x −y ;
(q )
x
y
= q xy .
Si
0 < q < 1, la fonction exponentielle de base q est strictement décroissante sur .
Si
q > 1, la fonction exponentielle de base q est strictement croissante
sur .
La
fonction exponentielle de base 1
est la fonction constante égale à 1.
Remarque
1
q = q 2 et q 0 = f (0 ) = 1.
Séquence 4 – MA01
41
© Cned - Académie en ligne
3. La fonction exponentielle
La
fonction exp est la fonction exponentielle dont le nombre dérivé en 0 est 1.
exp(1) = e avec e ≈ 2,7. On note exp( x ) = e x pour tout réel x.
La fonction exp vérifie toutes les propriétés du paragraphe précédent (en remplaçant q par e) :
Notamment :
z e x > 0, pour tout réel x.
zLa fonction exp est strictement croissante sur (elle conserve l’ordre :
a ≤ b ⇒ ea ≤ eb ).
1
z e x + y = e x × e y ; e − x =
;
ex
ex
e
y
= ex − y ;
( )
ex
y
= e xy .
La
fonction exp est continue et dérivable et la dérivée de la fonction exponentielle est elle-même : exp ′ = exp .
Tableau
de variations de exp et courbe :
x
exp ′( x )
−∞
0
+∞
+
exp(x )
1
exp
1
O
O
Si
1
u est une fonction dérivable sur un intervalle I, la fonction f définie sur I par
f ( x ) = eu ( x ) est alors dérivable sur I et pour tout x de I, f ′( x ) = u ′( x )eu ( x ) .
42
© Cned - Académie en ligne
Séquence 4 – MA01
6
Exercices
de synthèse
Exercice I
Etudier le sens de variations de la fonction f définie sur par f ( x ) = e x − x .
Exercice II
On injecte à un animal, par voie intramusculaire, 5 cm3 d’une substance. Cette
substance, normalement absente de son organisme, passe du muscle au sang
puis est éliminée au niveau des reins.
On admet que la quantité q (t ) en cm3 de cette substance présente dans le sang
à l’instant t (exprimé en minutes) est de la forme : q (t ) = C × e
−t
8
où C est une
constante.
Déterminer C.
Déterminer q ′(t ) pour t ≥ 0. Étudier les variations de la fonction q sur
[0 ; + ∞ [.
(
Déterminer la limite de la suite q (n )
)n ∈ .
Compléter le tableau de valeurs à 10−3 près :
t
0
q (t )
5
2
4
6
8
10
Représenter la fonction q sur [0 ; 10] dans un repère orthogonal :
en abscisse : 1 cm représente 1 minute ;
en ordonnée : 1 cm représente 0,5 cm3 .
Déterminer graphiquement (à l’aide de la courbe du . ou de la calculatrice)
le temps au bout duquel il reste dans le sang moins de 50 % de la substance
injectée.
Exercice III
2
Etude de la fonction f définie sur par f ( x ) = e − x .
Calculer f ′( x ).
Déterminer le signe de f ′( x ) sur .
Dresser le tableau de variations de f.
A l’aide de la calculatrice, représenter f sur l’intervalle [ −10 ; 10].
La courbe semble confondue avec l’axe des abscisses à partir d’une certaine
valeur. Est-ce le cas ?
Comment peut-on expliquer cette observation ?
Séquence 4 – MA01
43
© Cned - Académie en ligne
Exercice IV
(d’après bac ES – Métropole / La Réunion – septembre 2009)
On considère les fonctions f, g et h définies et dérivables pour tout nombre réel
x de l’intervalle [4 ; 6] par :
f ( x ) = 100(e x − 45), g ( x ) = 106 e − x , et h ( x ) = g ( x ) − f ( x ).
On note h ′ la fonction dérivée de la fonction h sur l’intervalle [ 4 ; 6].
On cherche à résoudre l’équation h ( x ) = 0.
a) Démontrer que la fonction h est strictement décroissante sur l’intervalle
[ 4 ; 6].
b) Dresser le tableau de variations de la fonction h.
c) Justifier que l’équation h ( x ) = 0 admet une solution unique α sur l’intervalle
[ 4 ; 6].
a) Recopier puis compléter le tableau de valeurs suivant (les résultats seront
arrondis à la centaine la plus proche) :
x
4
h( x )
17400
4,2
4,4
4,6
4,8
5
5,2
−3600
−8100
5,4
5,6
5,8
6
−25500
−33400
b) Sur la figure suivante, tracer la courbe représentative h de la fonction h
dans le plan muni d’un repère orthogonal :
y
20 000
16 000
12 000
8 000
4 000
0
4
–4 000
–8 000
–12 000
–16 000
–20 000
–24 000
–28 000
–32 000
–36 000
44
© Cned - Académie en ligne
Séquence 4 – MA01
4,2 4,4 4,6 4,8
5
5,2 5,4 5,6 5,8 6
6,2 6,4
x
c) Placer α sur ce graphique et en donner un encadrement d’amplitude 10−1.
Exercice V
Partie I
On considère la fonction g définie sur par g ( x ) = e x − x − 1.
Calculer g ′( x ) et étudier son signe.
Dresser le tableau de variations de g .
En déduire que pour tout réel x, e x ≥ x + 1.
Partie II
)
On considère la courbe de la fonction exp dans un repère orthonormé (O , I , J .
Déterminer une équation de la tangente à au point d’abscisse zéro.
Tracer et à l’aide de Geogebra.
Interpréter graphiquement l’inégalité de I.
Exercice VI
(d’après bac ES – Amérique du Sud – novembre 2010)
On considère la fonction numérique f définie et dérivable sur telle que, pour
tout réel x, on ait :
f (x ) =
x2
− x 2e x −1.
2
On note f ′ sa fonction dérivée sur .
Le graphique ci-après est la courbe représentative de cette fonction telle que
l’affiche une calculatrice dans un repère orthonormé.
y
1
O
x
Quelle conjecture pourrait-on faire concernant le sens de variations de f sur
l’intervalle [ −3 ; 2] en observant cette courbe ?
Dans la suite du problème, on va s’intéresser à la validité de cette conjecture.
Calculer f ′( x ) et vérifier que f ′( x ) = xg ( x ) où g ( x ) = 1− ( x + 2)e x −1 pour
tout x de .
Pour la suite, on admet que g est dérivable sur et on note g ′ sa fonction
dérivée.
Séquence 4 – MA01
45
© Cned - Académie en ligne
Étude du signe de g ( x ) suivant les valeurs de x.
a) Calculer la limite de la suite ( g (n )
)n ∈ .
b) Calculer g ′( x ) et étudier son signe suivant les valeurs du nombre réel x.
c) En déduire le sens de variations de la fonction g puis dresser son tableau de
variations.
d) Montrer que l’équation g ( x ) = 0 possède une unique solution dans [0 ; + ∞ [
On note α cette solution.
Justifier que 0, 20 < α < 0, 21.
e) Montrer que pour tout x ∈] − ∞ ; − 2], –(x + 2)ex–1 ≥ 0.
En déduire que pour tout x ∈] − ∞ ; − 2], g (x ) ≥ 1.
f) Déterminer le signe de g ( x ) suivant les valeurs de x.
Sens de variations de la fonction f
a) Étudier le signe de f ′( x ) suivant les valeurs de x .
b) En déduire le sens de variations de la fonction f.
c) Que pensez-vous de la conjecture de la question ?
46
© Cned - Académie en ligne
Séquence 4 – MA01
Q