I ] Forme algébrique

I ] Forme algébrique
1. Définitions
· Le nombre complexe i est tel que
· Un nombre complexe z s'écrit de façon unique
sous la forme a + bi ; a Î IR , b Î IR
£ = ensemble des nombres complexes ( ÌÌÌÌÌ¥¢¤¡£ID )
· On dit que a + bi est la forme algébrique du nombre complexe z.
a est la partie réelle de z, on note a = Re(z)
b est la partie imaginaire de z, on note b = Im(z).
· Les complexes de la forme bi avec b Î IR, sont appelés imaginaires purs.
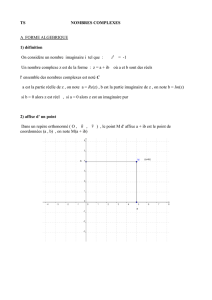
2. Représentation géométrique d'un nombre complexe
Le plan rapporté à un repère orthonormal direct (O;u;v)
rr
est appelé plan complexe. Au nombre
complexe z = a + bi , on peut associer le point M(a ; b) ou le vecteur uur w(a ; b).
§ L'axe des abscisses est appelé l'axe des réels
§ L'axe des ordonnées est appelé l'axe des imaginaires.
§ z = a + bi est l'affixe de M et de
uur
w.
§ M(a ; b) est l'image ponctuelle, uur w (a ; b) est l'image vectorielle de z = a + bi.
§ Le point Q (-a ; -b) , symétrique de M par rapport à O a pour affixe - z , opposé de z.
§ Le point N(a ; -b) , symétrique de M par rapport à l'axe des abscisses a pour affixe le nombre
complexe appelé conjugué de z et noté z.
Si z = a + bi alors z= a – bi .
§ Si M a pour affixe z = a + bi et si M' a pour affixe z' = a' + b'i , alors
le vecteur MM'
uuuuur
a pour affixe z' - z = (a' - a) + (b' - b)i
· le milieu I de [ ] MM' a pour affixe zI = 2'zz +
· le barycentre G de (M ; a) et (M ' ; b) a pour affixe zG = '
zz
ab
ab
+
+ (a
+ b ¹0) .
3. Propriétés dans £:
pour z = a + bi , z' = a' + b'i
· Deux nombres complexes sont égaux
si et seulement si, ils ont même partie réelle et même partie
imaginaire. : z = z' Û a = a' et b = b'
· Addition : z + z ' = (a + a' ) + i (b + b ' )
· Produit :
z z ' = (a a' – b b' ) + i (a b' + b a' )
· Inverse
: pour z non nul : 11abi
zabia²b²
-
==
++
· Quotient
: pour z' non nul : zabi(abi)(a'b'i)
z'a'b'ia'²b'²
++-
==
++
· Propriétés de i
: i² = -1 ; i3 = - i ; i4 = 1 ; 1i i
ii²
==- .
· Propriétés des nombres complexes conjugués
:
z= z ; zz'+ = z + z' ; zz'- =z - z' ; zz'
= z
z' ;
z z
= (a + bi) ( a – bi) = a² + b² est un réel positif ou nul.
Si z' # 0 11
z' z'
æö
=
ç÷
èø ;
zz
z' z'
æö
=
ç÷
èø
z est réel Û z = z
; z est imaginaire pur Û z = - z
i² = -1
Prof : Hadj Salem Habib
Lycée pilote Médenine
Page 1
Lycée pilote Médenine
Nombres complexes
Prof : Hadj Salem Habib

II] Forme trigonométrique
1. Module d'un
nombre complexe
·
Si le point M est l'image du complexe z = a + bi ( a Î IR , b Î IR) dans le plan complexe £, on appelle
module de
z ,noté z , la
distance OM
·
Propriétés
: |z| = 0 Û z = 0 ; |- z| = |z| ; |z + z'| £ |z| + |z'|
|zz'| = |z|.|z'| ; n
z=
zn
; zz=
Pour
z' non nul : 11z'
z'z'z'²
==
et z
z
z'z'
=
Si
M a pour affixe z et si M' a pour affixe z' alors OM = |z| et MM' = |z' - z|
Si u
r a
pour affixe z , alors IIuII
r=
|z|.
2. Argument d'un
nombre complexe
·
Définition
: Un argument du nombre complexe z non nul est une mesure de l'angle polaire du point
M
dans le plan complexe muni du repère(O;u;v)
rr ,
c'est à dire une mesure q de l'angle
orienté(u;OM)
uuuur
r.
Le
réel 0 n'a pas d'argument. Le nombre complexe i a pour module 1 et pour argument 2
p
+.
·
Propriétés :
L'argument
d'un nombre complexe z n'est pas unique, il est défini modulo 2p.
Si q
est un argument de z, on notera arg z = q [ ]
2p
ou arg z = q + 2kp (k Î ZZ )
On
appelle argument principal de z l'argument de z appartenant à ]-p ; p].
Tout
réel positif a un argument égal à 0.
Tout
réel négatif a un argument égal à p.
Tout
nombre imaginaire pur, de partie imaginaire strictement positive a un argument égal à 2
p
et tout
nombre
imaginaire pur, de partie imaginaire strictement négative a un argument égal à - 2
p.
Soit
z nombre complexe non nul : z = a + bi , zr= et arg z = q [ ]
2p
alors
ì=+
ï
í
q==q==
ï
î
ra²b²
aRe(z)bIm(z)
cos;sin
rzrz
équivaut à
=q
ì
í=q
î
arcos
brsin
Pour
z Î
CI *
et z' Î CI *, on a z = z' Û { |z|
= |z'|,arg z = arg z' [2p]
z
et z' étant deux nombres complexes non nuls on a :
·
arg(zz') = arg z + arg z' [2p] ; arg 1
z
= - arg z [2p]
·
arg z
z'
= arg z - arg z' [2p] ; Pour n entier : arg (zn) = n arg z [2p]
·
arg (z)
= - arg z [2p] ; arg (- z) = arg z + p [2p]
½z½
= OM = ²²ab+
ou z= zz
Page 2
Nombres complexes
Lycée pilote Médenine
Lycée pilote Médenine
Prof : Hadj Salem Habib
Prof : Hadj Salem Habib

3. Forme trigonométrique d'un nombre complexe non nul
Tout nombre complexe non nul z peut-
être écrit sous la forme :
avec q
Î IR et r Î IR*
+
C'est la forme trigonométrique de z.
r est le module de z, r = |z|
q est un argument de z.
Si z = r (cos q + i sin q) alors Re(z) = r cos q et Im(z) = r sin q.
z=
r (cos(-q) + i sin(-q)) ; - z = r (cos(q + p) + i sin(q + p)) ; et ))(sin)((cos
11
qq -+-= i
r
z
4. Utilisation en géométrie
La notion de distance correspond au module - La notion d'angle à l'argument.
A, B , C et D étant quatre points distincts d'affixes zA, zB , zC et zD dans (O;u;v)
rr
, alors :
· le vecteur AB
uuur
a pour affixe zB - zA ,
· AB = ½zB - zA½
· l'angle (u;AB)
uuur
r
a pour mesure arg(zB - zA) [2p]
· l'angle
(
)
uuuruuuur
AB;CD a
pour mesure arg(zD - zC) - arg(zB - zA) = æö
-
ç÷
-
èø
DC
BA
zz
arg zz
· Comment démontrer que trois points A, B et C sont alignés
:
Û CA
BA
zz
zz
æö
-
ç÷
-
èø
est un nombre réel Û l'angle
(
)
AB;AC
uuuruuuur
est nul
ÛCA
BA
zz
arg zz
æö
-
ç÷
-
èø
= 0 [p]
· Comment démontrer que les droites (AB) et (CD) sont orthogonales
:
Û DC
BA
zz
zz
æö
-
ç÷
-
èø
est un imaginaire pur
Û l'angle
(
)
AB;CD
uuuruuuur a
pour mesure 2
p
ou - 2
p
Û DC
BA
zz
arg zz
æö
-
ç÷
-
èø
=2
p [p]
III] Notation exponentielle
Tout nombre complexe non nul z de module r et d'argument q
peut s'écrire : z = r i
eq;
et
réciproquement, tout nombre complexe qui s'écrit z = r i
eq
ou z = r (cosq
+ i sinq) avec r >0 a pour
module r et pour argument q
+ 2kp.
On a : i
e1
q= et
Arg ( i
eq) = q.
z = r (cos q + i sin q) q
M
r = |z|
1
cos
q
sin q
Nombres complexes
Lycée pilote Médenine
Prof : Hadj Salem Habib
Page 3
Lycée pilote Médenine
Prof : Hadj Salem Habib

Equation zn=a, n > 1, aΣ
Théorème et définition_
Soit a un nombre complexe non nul d'argument 0 et n un entier naturel non nul. L'équation
zn = a admet dans C, n solutions distinctes définies par :
2k
in
k
z re
q+p
æö
ç÷
èø
=,
{ }
k 0,1,........,n 1Î-
, où r est le réel strictement positif tel que rn = |a|. Ces solutions sont appelées les racines
nièmes du nombre complexe a._
Le plan est muni d'un repère orthonormé direct
(
)
O,i,j
rr
Lorsque n ³ 3, les points images des racines nièmes de l'unité sont les sommets d'un
polygone régulier inscrit dans le cercle
()
O,r
z
.
Exemples d'équations de degré supérieur ou égal à 3
Théorème :_
Soit a1 ,a2,... et an des nombres complexes tels que an¹ 0 ; n ³ 2 .
Soit P(z) = an
zn+an-1
zn-1+.. .+a1z+a0.
Si z0
est un zéro de P, alors P(z)=(z-z0)g(z), où g(z) = anzn-1+bn-2
zn-2+... + b0, avec b0, b1 ,.. ., et bn-2
complexes.
IV] Equation dusecond degré àcoefficientréels
L'équation a.z²+ b.z + c= 0,où a, bet csontdesréels (avec a¹0) admetdansCI deuxsolutions
(éventuellementconfondues).Soit D= b²- 4ac lediscriminantdel'équation
·si D>0,lesdeuxsolutions sontréelles Z1= b2a
--D
et Z2= b2a
-+D
·si D=0,unesolution double Z1= Z2=(-b)/2a
·si D<0, onpeutécrire D=(id)² avec d Î IR,
lesdeuxsolutions sontalorsdesnombrescomplexes, (conjuguésl'undel'autre):
1bi
bi
z2a2a
---D
--d
== ; 2bibi
z2a2a
-+d-+-D
==
·Letrinôme az2+ bz + c sefactorisesouslaforme a(z- z1)(z- z2)
V]NombresComplexeset cercle
Le cerclede centreAd'affixe zAetderayonrestl'ensembledespoints M d'affixezvérifiant: ½z- zA½=
r doncune équationparamétriquede ce cercle est : z= zA+r i
eq
Formulesd'EULER :Pourtoutnombreréel qona:
i
eq=cosq + i sin q et i e-q
=cosq-isinq
alors: ii
ee
cos 2
q-q
+
q= et ii
ee
sin 2i
q-q
-
q=
Propriétés : r eiq. r' eiq'=r r' ei(q+q') ; i
11
r
re q=e-iq ; i
i'
re
r'e
q
q = r
r' ei(q-q')
FormuledeMOIVRE : pourtoutn ÎZZ , (eiq)n= einqou
(cos q+i sin q)n = cos (n q)+i sin (n q)
L'utilisation desformulesd'Euleretde Moivrepermetde linéariserlespolynômestrigonométriques,
c'està dire quele polynôme trigonométriques'écrit uniquementavecdestermesdelaforme
a cos(mq) et b sin(nq) avec a,b,m , net q des réels
Nombres complexes
Lycée pilote Médenine
Prof : Hadj Salem Habib
Page 4
Lycée pilote Médenine
Prof : Hadj Salem Habib

Translation :soitunetranslationdevecteur u
rd'affixe a; lepointM(d'affixe z)est transforméenun
pointM'(d'affixez')telque: MM'u=
uuuur rdonc z'-z = ad'où l'expressioncomplexed'unetranslationest
:z'=z + a;où aestl'affixedu vecteurdetranslation.
Homothétie :soitunehomothétiederapport ketde centre Wd'affixe w; lepointM(d'affixe z)est
transformé enunpointM'(d'affixez')telque: M'kMW=W
uuuuruuuur donc
z'- w=k(z- w)d'où l'expressioncomplexed'unehomothétie est : z' - w=k(z- w);
où westl'affixedu centreet klerapportde cettehomothétie.
Rotation :soitunerotationd'angle qetde centre Wd'affixe w; lepointM(d'affixe z)est transforméen
unpointM'(affixez')telque:l'angle
( )
M;M'WW
uuuuruuuur = q donc z'- w= e
iq
(z- w)d'où l'expression
complexed'unerotationest : z'- w= i
eq(z- w);
où westl'affixedu centreet ql'anglede cetterotation.
L'applicationquiau pointMd'affixezassocielepointM'd'affixe z'= z.eiq
où qestun nombreréelfixé, estlarotationde centreOetd'angle q.
VI] NombresComplexesetTransformation
Nombres complexes
Lycée pilote Médenine
Prof : Hadj Salem Habib
Page 5
Lycée pilote Médenine
Prof : Hadj Salem Habib