vecteurs exo enonces

Rappel sur le calcul vectoriel   
A.FIZAZI Univ-BECHAR LMD1/SM_ST
30
** EXERCICES
:         ! ! "#$  %& '( .
2.1
   ! "#
OXYZ
$% &
'()**+,,) *-./,) :
1
34 4
Vijk
=+ 3
2
23 4
Vijk
=+
3
3
53
Vijk
=+
.
)/8 9: *!;<= >?@A
1
V
&
2
V
3
V
.
B/
*'() C.;<= C%:$ >?@A
123
AV V V
=++
123
2
BVVV
=+
D/E!F G<HIH,) J@)<,) K' 8+F
13
CV V
=+
L/"H!?,) M),) >?@A
13
.
VV
*;)N,) OPQR -
HSP+T JU<VIH,).
/  
23
VV
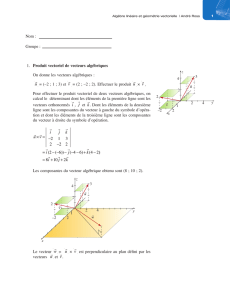
Exercice 2.1
On considère , dans un repère orthonormé OXYZ,
les trois vecteurs : 1
34 4
Vijk
=+ ,
2
23 4
Vijk
=+
et 3
53
Vijk
=+
.
a/ calculer les modules de
1
V
&
2
V
et
3
V
,
b/ calculer les composantes ainsi que les modules des
vecteurs :
123
AV V V
=++
et
123
2
BVVV
=+
,
c/ déterminer le vecteur unitaire porté par
13
CV V
=+
,
d/ calculer le produit scalaire
13
.
VV
et en déduire
l’angle formé par les deux vecteurs.
e/ calculer le produit vectoriel
23
VV
.
2.2
g)Uh iR 8 jhIk 8+Fl, m$n,) K<HH,)
x
y
z
A
AA
A
=
x
y
z
B
BB
B
= C+-)@oT HSPF $%H,)
Hp ",)<,) E!F *!+q?H,):
()
()
()
1/ 2
2
22
xx yy zz
SAB AB AB =+++++
()
()
()
1/2
2
22
xx yy zz
DAB AB AB =++
Exercice 2.2
Montrer que les grandeurs de la somme et de la
différence de deux vecteurs
x
y
z
A
AA
A
= et
x
y
z
B
BB
B
=
exprimées en coordonnées rectangulaires sont
respectivement :
()
()
()
1/2
2
22
xx yy zz
SAB AB AB =+++++
()
()
()
1/2
2
22
xx yy zz
DAB AB AB =++
2.3
     :
3
1
52 2
Vijk
=+
3
2
37
Vijk
=+
3
47 6
Vijk
=++
.
u SPVk ",) ;)N,)  *!VIH,) *!;<= >?@A
8 9:
,
OY OX
OZ
.
Exercice 2.3
Trouver la sommes des trois vecteurs :
1
52 2
Vijk
=+
32
37
Vijk
=+
3
3
47 6
Vijk
=++
.
Calculer le module de la résultante ainsi que les angles
qu’elle forme avec
,
OY OX
et
OZ
.
4.2:
)/"p K.w() gx)< *@? iA 8p$T
AB
y+@
A
B
gx)< "!w
8+Fl,) 8 9zlH,) K.w() .
Exercice 2.4
a/ Montrer que la surface d’un parallélogramme est
AB
tels que
A
et
B
sont les côtés du
parallélogramme formé par les deux vecteurs .
b/ Prouver que les vecteur
A
et
B
sont

Rappel sur le calcul vectoriel   
A.FIZAZI Univ-BECHAR LMD1/SM_ST
31
B/Kl,) iA 8p$T
A
E!F ;L<HF i<z;
Kl,)
B
*}.,) ~hhIk )•R
AB AB
+=
perpendiculaires si
AB AB
+=
5.2
i: )•RKl,) :
(
)
(
)
(
)
32 2
2232
V xy z i x y j xz k
=+++ + 
iA 8p$T
0
grad V V
= =
Exercice 2.5
Soit le vecteur :
(
)
(
)
(
)
32 2
2232
V xy z i x y j xz k
=+++ + 
Montrer que
0
grad V V
= =
2.6
iFl,) 8z+,
21
3
4
B ; A
==
8+F
,
Kl,) gx)<; y+IT
B
Kl,)
A
- &
HSP 9z, *h#)<H,) J@)<,) "F' 8+F .
Exercice 2.6
Soient les deux vecteurs
12
3
4
A , B
==
Trouver
,
pour que
B
soit parallèle à
A
,puis
déterminer le vecteur unitaire pour chacun des deux
vecteurs.
2.7
S,<= 8+F' *!VI 30HS uPVk  J@
8+;)x°25°50.
8+Fl,) *!;<= ‚A .
Exercice 2.7
La résultante de deux vecteurs a 30 unités de long et
forme avec eux des angles de 25° et 50°.
Trouver la grandeur des deux vecteurs.