1. Produit vectoriel de vecteurs algébriques On donne les vecteurs

Algèbre linéaire et géométrie vectorielle | André Ross 1
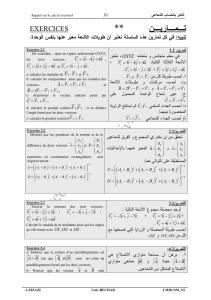
1. Produit vectoriel de vecteurs algébriques
On donne les vecteurs algébriques :
r
u
= (–2 ; 1 ; 3) et
r
v
= (2 ; –2 ; 2). Effectuer le produit
r
u
×
r
v
.
Pour effectuer le produit vectoriel de deux vecteurs algébriques, on
calcul le déterminant dont les éléments de la première ligne sont les
vecteurs orthonormés
r
i
,
r
j
et
r
k
. Dont les éléments de la deuxième
ligne sont les composantes du vecteur à gauche du symbole d’opéra-
tion et dont les éléments de la troisième ligne sont les composantes
du vecteur à droite du symbole d’opération.
u v
i j k
i j k
× = −
−
= − − − − − + −
2 1 3
2 2 2
2 6 4 6 4 2( ( )) ( ) ( ))
= + +8 10 2 i j k
Les composantes du vecteur algébrique obtenu sont (8 ; 10 ; 2).
1
x
y
2
2
–2
2 4
3
r
u
r
v
r
w
z
2
4
2
2
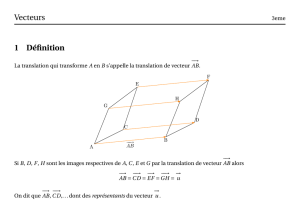
Le vecteur
r
w
=
r
u
×
r
v
est perpendiculaire au plan déni par les
vecteurs
r
u
et
r
v
.
Nom :
Groupe :
1
x
y
2
2
–2
2 4
3
r
u
r
v
z
2
4
2

2 Chapitre 8 | feuille d’exercices
2. Aire du parallélogramme
Calculer l’aire du parallélogramme construit sur les vecteurs
r
u
et
r
v
.
1
x
y
2
2
–2
2 4
3
r
u
r
v
r
w
z
2
4
L’aire du parallélogramme construit sur les vecteurs
r
u
et
r
v
est égale
au module du produit
r
u
×
r
v
.
Le module d’un vecteur de
°3
est égal à la racine carrée de la somme
des carrés des composantes.
u v× = + + = ≈8 10 2 168 12 96
2 2 2 ,
L’aire du parallélogramme à la racine carrée de 168 qui donne environ
12,96 unités de surface.
3. Hauteur du parallélogramme
Calculer la hauteur de ce parallélogramme abaissée sur le vecteur
r
v
ou son prolongement.
L’aire d’un parallélogramme est le produit de sa base par sa hauteur.
En divisant l’aire par la longueur de la base, on obtient donc la hau-
teur. Dans le cas présent, la base est le module du vecteur
r
v
, soit :
v= + − + =2 2 2 12
2 2 2
( )
En divisant l’aire par la longueur de la base, on obtient :
hu v
v
=×= =
168
12 14
On remarque que
u=14
et l’aire du parallélogramme est exacte-
ment le produit des modules des deux vecteurs. Cela signie que les
vecteurs
r
u
et
r
v
sont perpendiculaires comme le conrme leur produit
scalaire :
r
u
•
r
v
= (-2; 1; 3) • (2; –2; 2) = 0
Le parallélogramme est donc un rectangle.