Quotients et proportions

Chapitre 5
Quotients et proportions
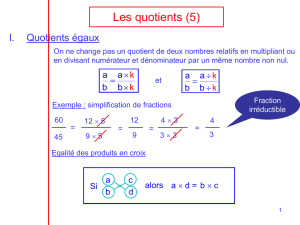
5.1 Quotients égaux
Définitions. Un quotient est le résultat d’une division. Le quotient de a par b
se note a
b. Si a et b sont des nombres entiers a best une fraction, le nombre a est
le numérateur, b est le dénominateur.
Remarques. a
a= 1 ; a 1= 1 ; 0 a= 0 avec a non nul
Règles. Le quotient de deux nombres ne change pas si on multiplie (ou on divise)
ces deux nombres par un même facteur.
12
16 =12 : 4 16 : 4 =3 4;5×3 7×5=3 7
5.2 Comparaison de quotients
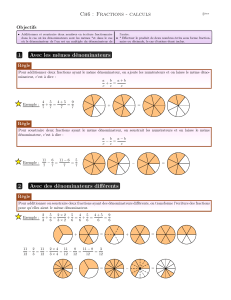
Règles. De deux fractions ayant des dénominateurs égaux, la plus grande est
celle dont le numérateur est le plus grand.
De deux fractions ayant des numérateurs égaux, la plus grande est celle dont le
dénominateur est le plus petit.
3
7<4 7;10 3>10 4
Méthodes. Pour comparer deux quotients on peut :
– calculer les quotients et comparer les nombres décimaux obtenus,
– écrire les quotients sous formes de fractions dont les dénominateurs sont égaux,
– Comparer ces quotients avec un même troisième nombre.
10

Exemple. Comparer 14/3 et 12/7
14
3>4et 12 7<2donc 14 3>12 7
5.3 Proportion et pourcentage
Vocabulaire. Une proportion est le quotient d’une quantité partielle par la
quantité totale. Un pourcentage est une proportion ramenée à un total de 100.
Exemple 1. Dans une classe de 24 élèves 6 élèves étudient le Latin. La quantité
partielle est 6 élèves, la quantité totale est 24 élèves, la proportion d’élèves étudiant
le Latin est 6/24 soit un quart.
Exemple 2. Un vêtement de 64€est soldé à 5%, cela signifie qu’on fait une
remise de 5/100 du prix, c’est à dire :
5
100 ×64 = 1 20 ×64 = 64 20 = 3,2€
5.4 Produit de fractions
Règle. Pour multiplier des fractions on multiplie les numérateurs entre eux et
on multiplie les dénominateurs entre eux.
Exemple. 2
7×3 5=2×3 7×5
Remarque. Pour multiplier une fraction et un nombre entier on peut écrire le
nombre entier sous la forme d’une fraction de dénominateur 1.
Exemple. 8×5
9=8 1×5 9=8×5 9
5.5 Somme de fractions
Règle. Pour additionner ou soustraire deux fractions dont les dénominateurs
sont égaux, on additionne les numérateurs et on garde le dénominateur commun.
Exemple. 2
3+5 3=7 3
Méthode. Pour additionner des quotients on les écrit sous formes de fractions
dont les dénominateurs sont égaux.

Exemple. 3
4+5 12 =3×3 4×3+5 12 =9 12 +5 12 =9+5 12