TD: Référentiel non galiléen : Forces d`inerties Relation

Un axe matériel Ox est animé par rapport à un axe vertical D
faisant un angle α avec lui, d'un mouvement de rotation
uniforme de vitesse angulaire ω. Soit M une particule de masse
m qui coulisse sans frottement sur l'axe Ox.
TD: Référentiel non galiléen : Forces d’inerties
Relation fondamentale de la dynamique, Energie
Exercice 1: Pendule dans une voiture
Exercice 2: Lancement d’un obus dans le référentiel terrestre
En un lieu A de latitude λ=48°,un canon tire un obus à la vitesse v0=300ms-1 suivant la verticale
ascendante Az. On désigne par Axyz un repère orthonormé lié à la terre. Ax étant dirigé vers le
nord. On néglige la résistance de l’air et la variation de g avec l’altitude. g=10ms-2.
1. Etudier le mouvement de l’obus en considérant le référentiel lié à la terre comme galiléen.
Quelle est l’altitude maximum atteinte par l’obus ?
2. Reprendre l’étude précédente en tenant compte de la force de coriolis et en considérant
l’expression de la vitesse obtenue à la question 1. comme une première approximation. Donner
une expression approchée de y à la date t.
3. A quelle distance de A l’obus retombe t-il?.
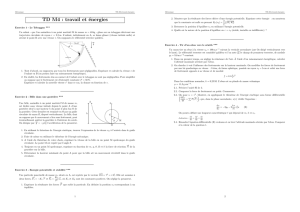
Exercice 3 : Mouvement d’un point matériel le long d’une tige en rotation
1. Déterminer la position d'équilibre relatif M0 de M. On pose Ω= ω sin(α).
2. M étant abandonné sans vitesse relativement à Ox à une distance a de M0, donner
l'expression de x en fonction du temps t. Quelle est la nature de la position d'équilibre M0:
stable ou instable? (on pourra présenter deux méthodes).
3. Calculer à l'instant t, la composante de l'action de M sur Ox perpendiculaire au plan .
Exercice.4: Mouvement d’un anneau sur un cerceau en rotation
Un fil de plomb de longueur l, de masse m=100g (figure 1) est
suspendu dans une automobile qui démarre sur une route horizontale
et droite, et acquiert une vitesse de 72kmh-1 sur l=100m.
L’accélération étant supposée constante sur le parcours, on demande
l’inclinaison du fil θeq par rapport à la verticale et sa tension. Trouver
l'équation du mouvement en θ; on pourra présenter deux méthodes.
Quelle est la période des petites oscillations quand on déplace la
masse m de sa position d’équilibre

Un anneau de masse m assimilable à un point matériel glisse sans frottement sur un cerceau en
rotation uniforme ω autour d'un diamètre vertical.
1. Déterminer les positions d'équilibre de l'anneau, étudier la stabilité de ces équilibres (deux
méthodes possibles).
2. Déterminer la période d'oscillation autour des positions d'équilibre stable.
Exercice 5: Equilibre d’une bille dans un tube en rotation
Exercice 6: Le sismographe
1. Ecrire la relation fondamentale de la dynamique dans R' et déduire l'amplitude X'm du
mouvement.
2. Tracer X'm= f(ω) et interpréter le résultat pour pouvoir analyser les secousses.
On considère un tube, dont la forme peut être décrite dans
le plan par l'équation y = ax2, tournant à la vitesse constante
ω autour de l'axe Oy. Une bille de masse m est introduite
dans le tube en un point donné sans vitesse initiale.
Calculer la valeur de ω pour que la bille soit en équilibre dans
le tube sachant que la bille peut glisser sans frottement.
Le sismographe est un dispositif qui a pour but de mesurer
les vibrations de la terre dues aux secousses sismiques. On
modélise le système par une boite dans laquelle on accroche
un ressort et une masse m. Le mouvement de la masse est
amorti par un frottement visqueux .
L'ensemble est posé sur la surface du sol. Le référentiel
terrestre est supposé galiléen. La surface de la terre a un
mouvement D(t) = D0 cos(ωt). Le référentiel R' lié à la boite
est donc non galiléen.

Eléments de réponse :
Ex.1 : accélération a=2ms-2 Le référentiel R lié a la voiture est en translation non uniforme, donc R’ est non
galiléen . Equation du mouvement dans R : Projection sur les vecteurs er et eθ :
On peut résoudre cet exercice avec le théorème de l’énergie mécanique. Le système est conservatif dans R,
l’énergie mécanique se conserve. Il faut déterminer l’énergie potentielle liée à la pesanteur, à la tension et à
la force d’inertie d’entrainement (Ep (tension) =Cte car la tension ne travaille pas, elle est perpendiculaire
au déplacement) et écrire que dEmécanique /dt=0. On trouve alors l’équation du mouvement.
On peut aussi obtenir l’équation du mouvement avec le théorème du moment cinétique dans un référentiel
non galiléen.
Ex.2 :1. En considérant le référentiel terrestre comme galiléen, le mouvement de l’obus est un rectiligne
suivant OZ :
2. Le référentiel terrestre n’est plus considéré comme galiléen et on admet que la vitesse est donnée par
. Les équations du mouvement sont :
.L’obus tombe z=0
y est positif, la déviation est vers l’ouest ce qui n’est pas en contradiction avec le cours lorsqu’on a vu qu’un
corps en chute libre était dévié vers l’est. Ici le corps n’est pas en chute libre car il est une vitesse initiale.
Ex.3 : Cet exercice peut être traité soit par la relation fondamentale de la dynamique dans le référentiel lié
à la tige qui est non galiléen et on la projette sur l’axe OX ( la composante de la force d’inertie de Coriolis
est donc nulle), soit à l’aide du théorème de l’énergie mécanique qui se conserve car la force de Corioslis et
la réaction de la tige sur M ne travaillent pas, la force d’inertie d’entraînement est conservative et le poids
est conservatif

Ex.4 : L’étude est faite dans le référentiel lié à l’anneau qui est non galiléen, les forces qui s’exercent sont
les forces d’inerties d’entrainement et de Coriolis (Ficoriolis ne travaille pas), la réaction du support qui ne
travaille pas et le poids. On peut traiter cet exercice soit en appliquant la relation fondamentale de la
dynamique dans le référentiel lié à l’anneau ,soit à l’aide du théorème de l’énergie mécanique, soit avec le
théorème du moment cinétique. On présentera ici la méthode avec le théorème de l’énergie mécanique.
Ex.5 : La bille est e n équilibre si
z
θ
x

Ex.5 : Etude dans le référentiel lié au tube, référentiel non galiléen. Système : La bille : point matériel M de
masse m. Les forces : Poids, réaction du support sur la masse qui est perpendiculaire au déplacement (au
vecteur T) car M se déplace sans frottements ; forces d’inerties d’entrainement et de coriolis. La bille est
en équilibre, donc la force d’inertie de coriolis est nulle. On projette la RFD sur le vecteur tangent T et le
vecteur normal N. On repère le point M par ses coordonnées (x, y=ax2)
Ex,6 : On écrit dans le référentiel R’ non galiléen , le PFD : les forces sont la tension du ressort , le poids ,
la force d’inertie d’entrainement et le frottement. On obtient :
€
m x
••
=− k ( x − l
0)+
mg − αx
•
− m (− D
••
)
x
••
+
α
mx
•
+
k
m
( x − l
0)=
g + D
••
on pose l
1=
l
0+
mg
ket X
= x − l
1
X
••
+
α
mX
•
+
k
mX
= D
••
=− ω
2cos(
ωt )
On utilise la méthode des complexes pour déterminer l’amplitude de X(t)=Xmcos(ωt+ϕ)
€
Xm =−
ω
2
D
0
ω
0
2−
ω
2+
jω
0
Qω
⇒ Xm =
ω
2
D
0
( ω
0
2−
ω
2)2+(
ω
0
Qω
)2
=
QD
0
(1−1
u
2)2
Q
2+1
u
2
=
QD
0
f ( u )
avec u =
ω
ω
0
df
du
=0⇒1
u
2=1−1
2 Q
2
il faut donc
€
1
u
2=1−1
2 Q
2≥0⇒
Q ≥1
2
⇒ ω
max =
ω
0(1−1
2 Q
2)
−1
2
Xm est croissante pour ω< ωmax et décroissante pour pour ω> ωmax avec Xm qui tend vers D0 pour ω qui
tend vers l’infini.. Donc pour des pulsations élevées, le système restitue les vibrations excitatrices. Quand il
y a un tremblement de terre, la pulsation du séisme ω>>>> ωmax Xm=D0 donc on mesure l’intensité du
séisme. Pour des pulsations beaucoup plus faible que ωmax, le système amortit les vibrations excitatrices.
Pour un véhicule en contact avec une route, (excitation : D0cos(ωt) on se place ω<<ωmax pour amortir au
maximum les oscillations de la route ?