chapitre5 1

'(8*69²8&%/
0$7+(0$7,48(6287,/63285/$%,2/2*,(
&KDSLWUH3ULPLWLYHV,QWpJUDWLRQ
Sandrine CHARLES (09/10/2001)
Introduction
Un exemple en Biologie
Vers d’autres sites…
1 Primitives
1.1 Définitions - Théorème fondamental
1.2 Primitives des fonctions usuelles
1.3 Linéarité
1.4 Fonctions composées
2 La notion d’intégrale
2.1 Intégrale d’une fonction
2.2 Intégrale et primitive
2.3 Premières propriétés
3 Intégrales et inégalités
3.1 Valeur moyenne d’une fonction sur un intervalle
3.2 Inégalités de la moyenne
3.3 Valeur absolue d’une intégrale
4 Méthodes de calcul exact d’intégrales
4.1 Utilisation des primitives usuelles
4.2 Intégration par décomposition en somme (linéarisation)
4.3 Changement de variable
4.4 Cas des fractions rationnelles
4.5 Cas simples de fonctions trigonométriques
4.6 Cas complexes de fonctions trigonométriques et hyperboliques
4.7 Intégrations par parties
4.8 Cas des fonctions de la forme
()
x
Pxe
α
avec
()
Px polynôme
4.9 Compléments

Mathématiques : Outils pour la Biologie – Deug SV1 – UCBL S. Charles (09/10/2001)
......................................................................................................................................................................................................
- Chapitre 5 : Primitives - Intégration, p2/27 -
5 Méthodes de calcul approché d’intégrales
5.1 Méthode des rectangles
5.2 Méthode des trapèzes
5.3 Autres méthodes
6 Applications du calcul intégral
7 Exemples d’application en Biologie
7.1 Un exemple en Démographie
7.2 Un exemple en Médecine

Mathématiques : Outils pour la Biologie – Deug SV1 – UCBL S. Charles (09/10/2001)
......................................................................................................................................................................................................
- Chapitre 5 : Primitives - Intégration, p3/27 -
&KDSLWUH3ULPLWLYHV²,QWpJUDWLRQ
,QWURGXFWLRQ
Ce chapitre repose sur les notions abordées aux chapitres 1 à 4, en particulier le chapitre 3 sur
les dérivées. Le chapitre 5 revient sur la définition des primitives et intégrales, et donne toute
une liste de « recettes » pour le calcul d’intégrales « non élémentaires ».
Le formulaire des primitives contient une liste des plus usuelles. Il est donc obligatoire de le
connaître. Le contenu du chapitre 5 permet d’aborder des intégrales jugées au premier abord
plus difficiles. Le programme de Deug SV correspond au premier niveau de lecture de ce
cours. Pour ceux qui voudrait aller plus loin, vous trouverez au travers de nombreux liens,
matière à vous satisfaire.
8QH[HPSOHHQ%LRORJLH
Tout au long de ce chapitre, nous essaierons d’illustrer les différentes notions abordées, en
traitant un exemple d’application en Médecine, dans lequel intervient la fonction suivante :
()
0.1
3t ft e
−
=
f est définie sur l’intervalle
[]
0;20 et relie la quantité d’un certain médicament dans le sang
après injection au temps t, pendant une période de 20h qui suit l’injection.
9HUVG·DXWUHVVLWHV«
http://perso.wanadoo.fr/math.15873/primitives.htm
 3ULPLWLYHV
Dans tout le chapitre 5, I désignera un intervalle fermé (ou segment) de \.
 'pILQLWLRQV7KpRUqPHIRQGDPHQWDO
Définition (primitive sur un intervalle) :
Soit une fonction :fI→\. On dit que :FI
→
\ est une primitive de f sur I si F est
dérivable sur I, et si xI∀∈
() ()
Fx fx
′=.
Exemple 1
Un exemple en Biologie

Mathématiques : Outils pour la Biologie – Deug SV1 – UCBL S. Charles (09/10/2001)
......................................................................................................................................................................................................
- Chapitre 5 : Primitives - Intégration, p4/27 -
Proposition (primitives d’une même fonction) :
Soit une fonction :fI→\ admettant une primitive F sur I. La fonction :GI→\ est aussi
une primitive de f sur I si et seulement si il existe une constante C∈\ telle que xI∀∈ ,
() ()
Gx Fx C=+.
Remarque : Une fonction ne peut pas avoir une seule primitive ; il est donc « interdit » de
parler de la primitive d’une fonction.
Démonstration
Exemple 3
Conséquence (primitive prenant une valeur donnée en un point) :
Soit une fonction :fI→\ admettant une primitive F sur I. Soient 0 xI∈ et 0 y∈\.
Il n’existe qu’une seule primitive G de f telle que
()
00
Gx y
= ; elle est donnée par
()
00
GFFx y=− +.
En particulier,
()
0
HFFx=− est l’unique primitive de f sur I qui s’annule en 0 x.
Remarque : La formule
()
0
HFFx=− peut paraître troublante…en effet, H est une fonction
bien définie et F est une quelconque des primitives de f : quel que soit le choix de F, H reste
inchangée.
Exemple 4
Un exemple en Biologie
Théorème fondamental :
Si :fI→\ est une fonction continue, alors elle admet une primitive (donc une infinité).
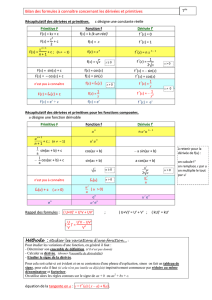
 3ULPLWLYHVGHVIRQFWLRQVXVXHOOHV
Le formulaire des primitives vous propose une liste de primitives des fonctions usuelles, qu’il
est impératif de connaître par cœur.
Exemples 5
¹ Nous allons voir dans la suite que la plupart des théorèmes que nous avons démontré pour
la dérivation (chapitre 3) fournissent des théorèmes sur les primitives.

Mathématiques : Outils pour la Biologie – Deug SV1 – UCBL S. Charles (09/10/2001)
......................................................................................................................................................................................................
- Chapitre 5 : Primitives - Intégration, p5/27 -
 /LQpDULWp
Nous avons vu que si f et g sont dérivables sur I, alors ,
αβ
∀∈
\ la fonction hfg αβ =+
est dérivable sur I avec hfg αβ
′′′
=+ (cf. chapitre 3, § 4.1).
Il en découle la proposition suivante :
Proposition :
Soient f et g deux fonctions définies sur un même intervalle I et admettant des primitives. Si F
est une primitive de f et G une primitive de g, alors, ,
αβ
∀∈
\, la fonction FG αβ + est une
primitive sur I de la fonction fg αβ +.
Cette proposition découle directement des propriétés de dérivation d’une somme de fonctions
et du produit d’une réel par une fonction (Chapitre 3, § 4.1).
Exemple 6
 )RQFWLRQVFRPSRVpHV
Nous avons également vu au chapitre 3 ( § 4.3) que si u est dérivable sur I et G dérivable sur
J, alors GuD est dérivable sur I et que xI∀∈ ,
()
()
()
() ()
()
Gux u xG ux
′′′
=.
La proposition suivante découle donc directement du théorème de dérivation des fonctions
composées :
Proposition :
Soient u une fonction dérivable sur un intervalle I, et g une fonction définie sur intervalle J tel
que xI∀∈ ,
()
ux J∈.
Si g admet une primitive G sur J, alors une primitive sur I de la fonction définie par
() () ()
()
fx ux gux
′
=× est la fonction F définie par
() ()
()
Fx Gux=.
Ce théorème, appliqué lorsque g est une fonction usuelle, permet de rechercher les primitives
de nombreuses fonctions f dérivables sur I. Exemple 7.