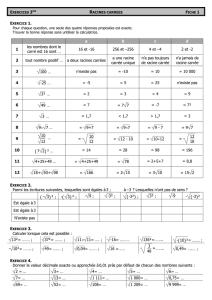
CCP Maths 2 MP 2005 — Corrigé

c Éditions H&K
Publié dans les Annales des Concours
1/14
CCP Maths 2 MP 2005 — Corrigé
Ce corrigé est proposé par Hicham Qasmi (ENS Lyon) ; il a été relu par Guillaume
Dujardin (ENS Cachan) et Paul Pichaureau (Professeur en CPGE).
Ce sujet aborde le thème des racines carrées de matrices. Il porte essentiellement
sur l’étude de leur existence et sur les propriétés topologiques de l’ensemble qu’elles
constituent. Il est composé de trois parties indépendantes.
• La première partie permet de déterminer les racines carrées de quelques
matrices simples. Elle fait appel à des notions de base en algèbre linéaire,
et plus précisément sur la réduction des matrices.
• La deuxième porte sur l’étude de quelques propriétés topologiques des racines
carrées de matrices : forment-elles un ensemble fermé ? borné ?
• Enfin, la troisième partie propose de déterminer l’intérieur de l’ensemble des
racines carrées de matrices en introduisant un ensemble bien choisi de
polynômes dont on étudie les racines.
Dans l’ensemble, le sujet est de longueur raisonnable et ne présente pas de grande
difficulté. Il a l’avantage d’être assez complet car il fait appel à des outils d’algèbre
(la réduction de matrices et les polynômes) et de topologie (les espaces vectoriels
normés).
Téléchargé gratuitement sur www.Doc-Solus.fr .
c Éditions H&K
Publié dans les Annales des Concours
2/14
Indications
Première partie
2.b Utiliser le résultat de la question précédente.
2.d Exploiter le calcul de la question précédente.
3 On pourra utiliser les résultats des questions 1, 2.d et 2.e.
4 Appliquer le résultat de la question précédente. Puis, pour rendre les calculs plus
aisés, remarquer que A est symétrique et possède des valeurs propres simples.
5.a Penser à la formule du rang.
5.b Garder à l’esprit que cette base de Im f est aussi une famille de vecteurs
de Ker f .
6.a Utiliser le résultat de la question précédente.
6.b Quelles sont les valeurs possibles de r ?
7.b Trouver un polynôme annulateur de R.
8 Utiliser la question précédente.
9 Utiliser la question 2.d.
10 On s’inspirera de la réponse à la question 3.
Deuxième partie
11 Écrire Rac(A) comme l’ensemble des zéros d’une fonction bien choisie.
12.b S’inspirer de la preuve de la question précédente.
12.c Se souvenir de la question 7.a.
Troisième partie
13 Penser à la définition de la norme infinie sur Rp .
15.a Utiliser la question 14.a.
15.b Utiliser les questions 13.a puis 15.a.
15.c Utiliser la question précédente.
16.b Appliquer le résultat des questions 13.b et 15.c.
Téléchargé gratuitement sur www.Doc-Solus.fr .
c Éditions H&K
3/14
Publié dans les Annales des Concours
I. Détermination de Rac(A) dans
quelques exemples simples
1 La matrice A est réelle de taille n et possède exactement n valeurs propres réelles
distinctes ; elle est donc diagonalisable, c’est-à-dire
∃P ∈ GLn (R)
A = PDP−1
où D = diag(λ1 , . . . , λn ).
Supposons que R soit une racine carrée de A. Comme
∃P ∈ GLn (R)
on a
A = PDP−1
S2 = P−1 RP
2
= P−1 RPP−1 RP
= P−1 R2 P
car R ∈ Rac(A)
= P−1 AP
S2 = D
Autrement dit, S est une racine carrée de D.
Réciproquement, si la matrice S est une racine carrée de D, alors
2
R2 = PSP−1
= PSP−1 PSP−1
= PS2 P−1
car S ∈ Rac(D)
= PDP−1
R2 = A
donc R est une racine carrée de A. Finalement,
R ∈ Rac(A)
⇐⇒
S ∈ Rac(D)
2.a Soit S une racine carrée de D. Il vient que
DS = S2 S = SS2 = SD
Les matrices S et D commutent.
2.b Pour toute matrice M, notons mij son coefficient (i, j). Le coefficient (i, j)
de la matrice DS − SD s’écrit
n
n
P
P
dik skj −
sik dkj = (λi − λj ) sij
k=1
k=1
Par ailleurs, les valeurs propres λ1 , . . . , λn sont deux à deux distinctes, donc
2
∀(i, j) ∈ {1, . . . , n}
i 6= j =⇒ sij = 0
La matrice S est donc diagonale.
Téléchargé gratuitement sur www.Doc-Solus.fr .
c Éditions H&K
Publié dans les Annales des Concours
4/14
2.c S est une racine carrée de D donc S2 = D. Or S est diagonale, si bien que
∀i ∈ {1, . . . , n}
si 2 = λi
2.d Soit R une racine carrée de A. D’après la question 1, S = P−1 RP est
alors une racine carrée de D = diag(λ1 , . . . , λn ). De plus, d’après la question 2.c,
S est forcément diagonale et ses coefficients diagonaux vérifient
∀i ∈ {1, . . . , n}
Ainsi,
∀i ∈ {1, . . . , n}
si 2 = λi
λi > 0
Une condition nécessaire pour qu’il existe une racine carrée de A est que toute valeur
propre de A soit positive ou nulle. La contraposée s’écrit alors
Si A admet une valeur propre strictement
négative alors Rac(A) est l’ensemble vide.
2.e Soit S une racine carrée de D. D’après la question 2.c,
∀i ∈ {1, . . . , n}
donc
∀i ∈ {1, . . . , n}
si 2 = λi
∃εi ∈ {−1; 1}
√
si = εi λi
√
√
n
Réciproquement, soient (ε1 , . . . , εn ) ∈ {−1; 1} et S = diag(ε1 λ1 , . . . , εn λn ).
Le carré de S est
S2 = diag ε1 2 λ1 , . . . , εn 2 λn = D
Ainsi,
n
Rac(D) = S ∈ Mn (R) | ∃(εi )16i6n ∈ {−1; 1}
√
√ S = diag ε1 λ1 , . . . , εn λn
3 Si A admet une valeur propre strictement négative alors, d’après la question 2.d,
Rac(A) est vide.
Sinon, considérons R une matrice de Mn (R). D’après la question 1, S = P−1 RP
est une racine carrée de D si et seulement si R est une racine carrée de A, donc
Rac(A) = PSP−1 S ∈ Rac(D)
où Rac(D) est donné par la question précédente. Comme λ1 < λ2 < . . . < λn ,
• soit λ1 est nul, auquel cas Rac(A) possède exactement 2n−1 éléments ;
• soit λ1 n’est pas nul, auquel cas Rac(A) possède exactement 2n éléments.
En conclusion,

 0
2n−1
card Rac(A) =
 n
2
si une valeur propre de A est strictement négative
si 0 est la plus petite valeur propre de A
sinon
Téléchargé gratuitement sur www.Doc-Solus.fr .