Histoire La géométrie étudiée au collège est la géométrie

6
ème
CHAPITRE 8
DROITES SECANTES, PERPENDICULAIRES ou PARALLELES
I. Droites parallèles, sécantes, perpendiculaires
1. Droites sécantes
Définition Deux droites sécantes sont deux droites ayant un seul point commun.
Exemple 1 Les droites (d) et (d’) sont sécantes en A.
On dit aussi : « Les droites (d) et (d’) se coupent en A. »
« Le point d’intersection des droites (d) et (d’) est A. »
Exemple 2 Les droites (AB) et (CD) sont sécantes.
En effet, on peut prolonger la droite (AB)…
2. Droites perpendiculaires
Définition Deux droites perpendiculaires sont deux droites qui se coupent
en formant quatre angles droits.
Exemple 3 « Les droites (d) et (d’) sont perpendiculaires. »
On utilise une équerre pour tracer des droites perpendiculaires.
Notation Le symbole « ⊥
⊥⊥
⊥ » signifie « est perpendiculaire à »
Codage On ne code qu’un seul angle droit.
Remarque - Deux droites perpendiculaires sont sécantes.
- Deux droites sécantes ne sont pas toujours perpendiculaires
(voir les exemples 1 et 2 ci-dessus)
3. Droites parallèles
Définition Deux droites parallèles sont deux droites qui ne sont pas sécantes.
Notation Le symbole « // » signifie « est parallèle à »
Exemple 4 Les droites (d) et (d’) sont parallèles.
Autrement dit, les droites (d) et (d’) n’ont
aucun point commun, même si on les prolonge…
On note : (d) // (d’)
Histoire La géométrie étudiée au collège est la géométrie euclidienne
géométrie euclidiennegéométrie euclidienne
géométrie euclidienne du savant grec Euclide
EuclideEuclide
Euclide vivant à
Alexandrie au 3
e
siècle avant J.C.
Il en a fondé les postulats (points de départ) :
« - Deux droites non parallèles se croisent en un point et un seul. »
« - Il existe qu’une seule droite passant par un point et parallèle à une autre droite. »
Le mot « Géométrie» vient des mots grecs « geo » (terre) et « metron » (mesure).
(d) (d')
A
ABC
D
(d) (d')
(d')
(d)
On code des droites
perpendiculaires
(d’) se dit
« d prime »

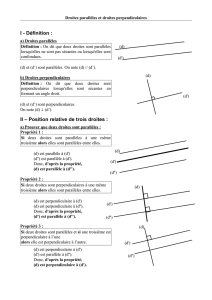
II. Propriété d’orthogonalité et de parallélisme
Propriété n°1 Propriété n°2 Propriété n°3
Les DONNEES
ou
Ce que l’on sait au
début du problème…
Donnée n°1 : (d2) ⊥
⊥⊥
⊥ (d1)
Donnée n°2 : (d3) ⊥
⊥⊥
⊥ (d1)
Donnée n°1 : (d2) // (d1)
Donnée n°2 : (d3) ⊥
⊥⊥
⊥ (d1)
Donnée n°1 : (d2) // (d1)
Donnée n°2 : (d3) // (d1)
La FIGURE
La CONCLUSION
ou
Ce que l’on peut
dire des droites
(d2) et (d3)…
(d2) // (d3)
(en gras sur la figure)
(d2) ⊥
⊥⊥
⊥ (d3)
(en gras sur la figure)
(d2) // (d3)
(en gras sur la figure)
La PROPRIETE
ou
Ce que l’on peut
utiliser pour justifier
en géométrie
Si deux droites sont perpendiculaires
à une même troisième,
alors elles sont parallèles entre elles.
Si deux droites sont parallèles,
alors toute perpendiculaire à l’une
est perpendiculaire à l’autre.
Si deux droites sont parallèles à une
même troisième,
alors elles sont parallèles entre elles.

III. Constructions…
1. Construire une perpendiculaire passant par un point
Animations en ligne : Construire une perpendiculaire passant par un point hors de la droite
Entrainements en ligne : Passer le permis Equerre
2. Construire une parallèle passant par un point
Animations en ligne : Construire une perpendiculaire passant par un point hors de la droite
IV. La médiatrice d’un segment
Définition La médiatrice d’un segment est la droite perpendiculaire à
ce segment et qui passe par le milieu de ce segment.
Exemple La droite (d) est la médiatrice du segment [AE] :
• (d) est perpendiculaire à [AE] ;
• (d) coupe le segment [AE] en son milieu I.
Remarque On peut « plier sur lui-même » le segment [AE] selon la droite (d).
On dit que la droite (d) est un axe de symétrie du segment [AE].
d
A
d
A
d
A
d
A
1
4
3
2
d
A
d
A
d
A
d
d
A
1
6
4
3
2
5
A
d
A

V. Des figures particulières…
1. Le trapèze
Définition Un trapèze est un quadrilatère qui a deux côtés parallèles.
Figure
2. Le rectangle
Définition Un rectangle est un quadrilatère qui a ses quatre angles droits.
Figure
Remarque Un rectangle a ses côtés opposés parallèles.
3. Le carré
Définition Un carré est un quadrilatère qui a ses quatre angles droits et ses quatre côtés de même longueur.
Figure
Remarques - Un carré a ses quatre angles droits, donc c’est aussi un rectangle particulier.
- Un carré a ses quatre côtés de même longueur, donc c’est aussi un losange particulier.
- Un carré a aussi ses côtés opposés parallèles
4. Le triangle rectangle
Définition Un triangle rectangle est un triangle qui a un angle droit.
Figure
Le triangle SOP est un triangle rectangle en S.
A
B
D
C
FG
H
I
K
L
M
N
O
P
S
Les côtés opposés sont parallèles