serie corrige primitive bac eco gestion

Mr :Khammour.K
Année Scolaire :2013/2014
Série n°6 : Primitive
4ème Eco-Gestion
Tél :[phone]
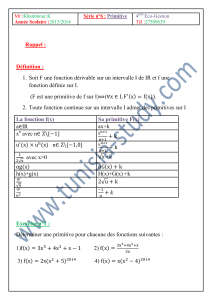
Rappel :
Définition :
1. Soit F une fonction dérivable sur un intervalle I de IR et f une
fonction définie sur I.
(F est une primitive de f sur I)(    .
2. Toute fonction continue sur un intervalle I admet des primitives sur I
La fonction f(x)
Sa primitive F(x)
aIR
ax+k
xn avec n 
   n 
 avec x>0
 +k
h(x)+g(x)
H(x)+G(x) +k
Exercice n°1 :
Déterminer une primitive pour chacune des fonctions suivantes :
1)      2) 
3)    4)   

5) 
 6) 
7) 
 8) 
Exercice n°2 :
Soit f la fonction définie par 
1) Déterminer les réels a et b tels que pour tout x de IR\{-1} on a :
2) a)Justifier que f admet une primitive sur ]-1,.
b)Déterminer une primitive F de f sur ]-1,.
c)Déterminer la primitive F de f tel que F(0)=0.
Exercice n°3 :
Soit f la fonction définie sur ]-3, par 
. Soit F la primitive de
f sur ]-3, tel que F(0)=0 .
1) Etudier les variations de la fonction F sur ]-3,.
2) Etudier le signe de F(x) sur ]-3,.
3) Soit g la fonction définie sur ]-3, par g(x)=F(x)-x.
a) Démontrer que g est décroissante sur]-3,.
b) En déduire que :si x>0 , alors F(x)<x.
Exercice n°4 :
Soit f la fonction définie sur ]-, par 
1) Justifier que f admet une primitive F sur ]-,.
2) Déterminer les réels a et b tels que pour tout réel x de ]-,,
3) En déduire la primitive F de f sur ]-, tel que F(-3)=1.

Correction des exercices :
Exercice n°1 :
1)       
2) 
3)    
4)   
5) 
6) 
7) 
8) 
Exercice n°2 :
1) 
Conclusion : a=3 et b=2
2) a) f est continue sur IR\{-1} en particulier sur ]-1,[ donc f admet une
primitive sur ]-1,[.
b) On a   
+k
c)    
+k et F(0)=0          
Conclusion :   
+2

Exercice n°3 : Soit f la fonction définie sur ]-3, par 
. Soit
F la primitive de f sur ]-3, tel que F(0)=0 .
1) F est la primitive de f sur ]-3,   
     0
 Si x    : F est décroissante.
 Si x   F est croissante.
2) F représente un minimum égale à 0 donc f est positive sur ]-3,.
3) Soit g la fonction définie sur ]-3, par   
a)g’(x)=F’(x)-1= 
   donc g est strictement décroissante sur
]-3,.
c) Si x>0 alors g(x)<g(0) c'est-à-dire que F(x)-x<F(0)-0=F(0)=0
Donc F(x)-x<0 F(x)<x.
Exercice n°4 :
  ]-,.
1) f est continue sur ]-, alors elle admet une primitive F sur
]-,[
2) 
 a=1 ;b=2
3) On a   
+k
+k et F(-3)=1            
+1