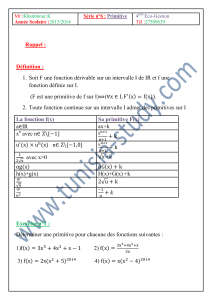
Savoir-faire fondamentaux Primitives

Savoir-faire fondamentaux
Primitives
• Toutes les questions commencent par « Je dois, sans hésiter, savoir ».
• Il s’agit le plus souvent de techniques simples de calcul.
• La liste proposée n’est en aucun cas exhaustive.
• Etre incapable de traiter une question vous mènera inévitablement à d’importantes déconvenues.
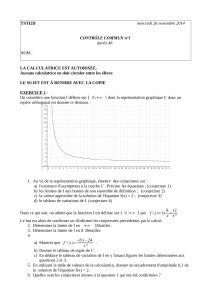
S.F. 1)Correction
déterminer une primitive de la fonction fdéfinie sur R
par :
f(x) = 2x3−3x+ 4.
S.F. 2)Correction
déterminer une primitive de la fonction fdéfinie sur R∗
par :
f(x) = 2
x2−1 x3.
S.F. 3)Correction
déterminer la primitive Fde la fonction fdéfinie sur R
par :
f(x) = x2−3exet F(0) = 5.
S.F. 4)Correction
montrer que la fonction x7→ (x−1)exest une primitive
sur Rde la fonction x7→ xex
S.F. 5)Correction
déterminer une primitive de la fonction fdéfinie sur R
par :
f(x) = 3e4x.
S.F. 6)Correction
déterminer une primitive de la fonction fdéfinie sur R
par :
f(x) = (2x+ 3) x2+ 3x−43.
S.F. 7)Correction
déterminer une primitive de la fonction fdéfinie sur R
par :
f(x) = x
√x2+ 1.
S.F. 8)Correction
déterminer une primitive de la fonction fdéfinie sur R
par :
f(x) = 4x3+ 2x
(x4+x2+ 1)3.

S.F. 1) Enoncé
F(x) = 1
2x4−3 2x2+ 4x

S.F. 2) Enoncé
F(x) = 2 ×−1
x−−1 2×1 x2=1 2x2−2 x

S.F. 3) Enoncé
Les primitives de fsont les fonctions Fkdéfinie sur R, telles que : Fk(x) = 1
3x3−3ex+k, avec k∈R.
On a alors : Fk(0) = −3 + k. Ainsi Fk(0) = 5 ⇐⇒ −3 + k= 5 ⇐⇒ k= 8.
Finalement : Fk(x) = 1
3x3−3ex+ 8.

S.F. 4) Enoncé
On note fla fonction définie sur Rpar : f(x) = (x−1)ex.
La fonction fest le produit d’un polynôme par la fonction exponentielle et est donc dérivable sur R.
De plus (uv)′=u′v+uv′, donc f′(x) = 1 ×ex+ (x−1)ex=ex+xex−ex=xex.
Donc fest une primitive sur Rde la fonction x7→ xex.