TRIANGLES et DROITES REMARQUABLES I/ CONSTRUCTIONS DE TRIANGLES

Chapitre 5
TRIANGLES et
DROITES REMARQUABLES
I/
CONSTRUCTIONS DE TRIANGLES
Quand on connait les longueurs des trois côtés. Construction vue en 6ème.
Quand on connait la longueur d’un côté et deux angles.
Exemple : construire le triangle ADE tel que : AD = 5cm DAE = 30° ADE = 50°
1. On trace le segment [AD].
2. On construit avec la règle et le rapporteur
une demi-droite d’origine A qui fait un
angle de 30° avec la demi-droite [AD).
3. On construit avec la règle et le rapporteur
une demi-droite d’origine D qui fait un
angle de 50° avec la demi- droite [DA).
4. Le point d’intersection des deux demi- A
droites est le point E.
E
D
Quand on connait un angle et deux longueurs
Exemple : construire le triangle CFG tel que : CF = 6cm
1. On trace le segment [CF].
2. On construit avec la règle et le rapporteur
une demi-droite d’origine F qui fait un angle
de 40° avec la demi-droite [FC).
3. On place le point G sur cette demi-droite de
sorte que : FG = 4cm.
4. On trace [CG].
FG = 4cm CFG = 40°
G
C
F
II/ HAUTEUR D’UN TRIANGLE
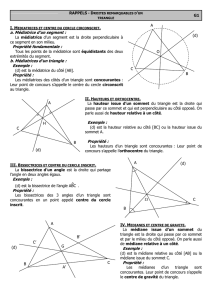
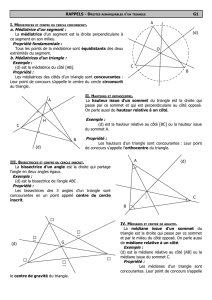
Définition : Dans un triangle, une hauteur est une droite qui passe par un
sommet et qui est perpendiculaire au côté opposé à ce sommet.
AP est appelée la hauteur
du triangle ABC.
Sommet dont est issue la hauteur
A
(d) est appelée la
hauteur issue de A.
On peut également dire
que (d) est la hauteur
relative au côté [BC].
B
C
P
P est appelé le Pied de la hauteur
(d)
Propriété (admise):
Les trois hauteurs d’un triangle sont concourantes en
un point H, appelé l’orthocentre du triangle.
A
A
H
C
B
B
H
III/ MÉDIATRICE ET CERCLE CIRCONSCRIT
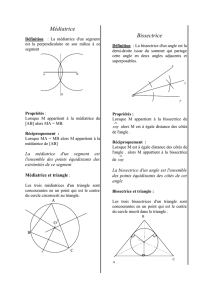
1°/
Médiatrice d’un segment
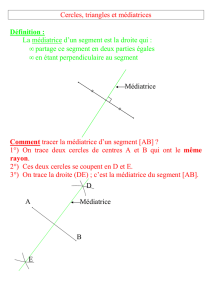
Définition : On appelle médiatrice d’un segment, la droite qui coupe ce
segment perpendiculairement en son milieu.
C
Construction de la médiatrice d’un segment
I
Soit [AB] un segment.
1. On trace deux arcs de cercles de même rayon
(rayon supérieur à la moitié de AB) de centres A et B.
Ils se coupent en deux points.
2. On trace (IJ). C’est la médiatrice de [AB].
A
B
J
Propriété : Si un point appartient à la médiatrice d’un segment
Alors il est équidistant des extrémités de ce segment.
Autrement écrit : Si I  (d) médiatrice de [AB] alors IA = IB
(d)
I
A
B
Propriété réciproque
Si un point est équidistant des extrémités
d’un segment,
alors ce point appartient à la médiatrice de
ce segment.
Autrement écrit : Si IA = IB alors I appartient à la médiatrice de [AB].
2°/
Cercle circonscrit (cercle qui passe par tous les sommets)
Propriété : Les trois médiatrices des côtés d’un triangle sont concourantes
en un point O, appelé le centre du cercle circonscrit au triangle.
Démonstration : Soit O le point d’intersection de (d1) et (d2 )
D’après les propriétés des médiatrices, on a : OA = OB et OB = OC
D’où OA = OC. Donc O  (d3) médiatrice de [AC].
OA = OB = OC Donc O est le centre du cercle circonscrit au
triangle ABC
A
(d2)
(d1)
(d3)
C
B
O
IV/ MÉDIANES
A
Définition : On appelle médiane d’un triangle,
la droite qui passe par un sommet
et le milieu du côté opposé à ce
sommet.
C
B
Propriété (admise): Les trois médianes d’un triangle sont concourantes en un
point G, appelé le centre de gravité du triangle.