Chap.4 Triangles

Chap.4 Triangles
1) Inégalité triangulaire.
a) Propriété.
Dans un triangle la longueur d’un côté (pris au hasard) doit
être inférieure à la somme des longueurs des 2 côtés restants.
b) Exemple1.
Tracez LBC tel que LB =2cm, BC=4cm, CL=5cm.
Est-il faisable ?
LB<LC+CB?
2<5+4 vraie
BC<BL+LC?
4<2+5 vraie
Donc LBC existe
CL<CB+BL?
5<4+2 vraie
c) Exemple2.
Tracez POM tel que PO =6cm, OM=2cm, MP=3cm.
Est-il faisable ?
PO < PM + MO?
6 < 3+2 fausse
OM < OP+PM?
2< 6+3 vraie
Donc POM n’existe pas
MP < MO+OP ?
3< 2+6 vraie
d) Remarque.
Dire que AB+BC=AC, revient à dire que B [AC].
2) Somme des angles dans un triangle.
a) Propriété.
Dans un triangle la somme des trois angles est égale à 180°
b) Exemple.
Un élève propose de tracer un triangle en fixant des valeurs aux 3 côtés. Mesure par la
classe puis par un logiciel de géométrie des 3 angles.
c) Cas particulier du triangle rectangle
 Angles complémentaires
Exemple 27° et 63° sont complémentaire car 27°+63°=90°
 Propriété.
Dans un triangles rectangle les 2 angles aigus sont
complémentaires.
 Exemple :
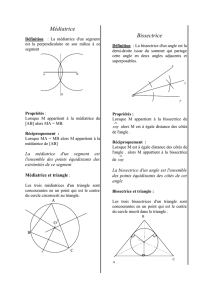
3) Médiatrice d’un segment.
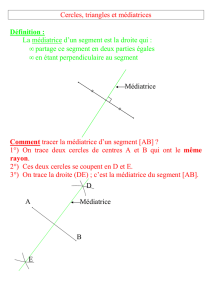
a) Définition.
La médiatrice d’un segment est la droite qui
1) passe par le milieu du segment
2) Est perpendiculaire au segment.

(d) passe par le milieu
de [AB] et (d)
perpendiculaire à [AB],
donc (d) est la
médiatrice du segment
[AB].
b) Propriété1.
Si un point appartient à la médiatrice d’un segment alors ce point est équidistant
des extrémités du segment.
(d) est la médiatrice de [AB]
M
(d) donc MA=MB
c) Propriété2.
Si un point est équidistant des extrémités d’un segment alors il appartient à la
médiatrice du segment.
Le point C est à égale distance des extrémités A et B du segment [AB], donc le
point C est sur la médiatrice de [AB].
De même pour le point D.

Donc (DC) est la médiatrice de [AB].
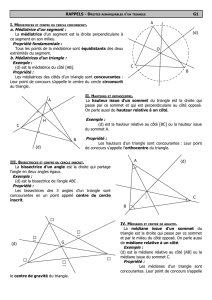
4) Médiatrices d’un triangle.
a) Exemple
b) Propriétés
 Dans un triangle les 3 médiatrices sont concourantes (se
coupent en même point).
 Le point d’intersection des 3 médiatrices est équidistant des 3
sommets
 Le point d’intersection des 3 médiatrices est le centre du cercle
circonscrit au triangle. (passe par les 3 sommets)
5) Hauteurs
a) Définitions
Une hauteur d’un triangle est une droite qui
 Passe par un sommet
 Et elle est perpendiculaire au côté opposé.
b) Exemple.
c) Propriété
Dans un triangle, les 3 hauteurs sont concourantes.
6) Médianes
a) Définitions
Une médiane dans un triangle est une droite qui
1) Passe par un sommet
2) Passe par le milieu du côté opposé.

b) Exemple
c) Propriétés
 Les 3 médianes sont concourantes.
 Le point de concours est le centre de gravité du triangle. (bonus)
7) Bissectrices. Voir 6ème et 4ème. Rappel en option.
c) Définitions
La bissectrice d’un angle est l’axe de symétrie de cet angle.
d) Exemple