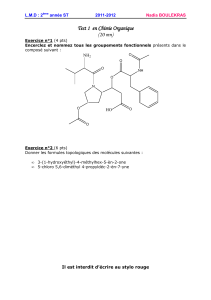
Corrigé du Contrôle Intermédiaire

E.S.I. Novembre 2012
1CPA et 1CPB.
Module : Algèbre I.
Corrigé du Contrôle Intermédiaire
Exercice 1 : (14 pts)
Sur l’ensemble R, on considère la loi de composition suivante :
x∗y=x+y−xy pour tous x, y ∈R.
I/ 1- Soient x, y ∈R\ {1}. Montrer que x+y−xy 6= 1.
Soient x, y ∈R\ {1}et supposons que x∗y= 1.
x∗y= 1 ⇐⇒ x+y−xy = 1
⇐⇒ x(1 −y) + y−1 = 0
⇐⇒ (1 −y)(x−1) = 0
⇐⇒ y= 1 ou x= 1.
D’où x∗y6= 1 car par hypothèse x6= 1 et y6= 1.(1 pts)
2- Montrer que (R\ {1},∗)est un groupe abélien.
i) On déduit de la question précédente que ∗est une LCI dans R\ {1}.(0,5 pts)
ii) Soient x, y, z ∈R\ {1}:
(x∗y)∗z= (x+y−xy)∗z
= (x+y−xy) + z−(x+y−xy)z
=x+y−xy +z−xz −yz +xyz
=x+ (y+z−yz)−xy −xz +xyz
=x+ (y∗z)−x(y+z−yz)
=x+ (y∗z)−x(y∗z)
=x∗(y∗z).
D’où ∗est associative. (1 pts)
iii) Soient x, y ∈R\ {1}:
x∗y=x+y−xy
=y+x−yx
=y∗x.
D’où ∗est commutative. (0,5 pts)
iv) Supposons qu’il existe e∈R\ {1}tel que pour tout x∈R\ {1}:x∗e=x, alors :
x∗e=x⇐⇒ x+e−xe =x
⇐⇒ e−xe = 0
⇐⇒ e(1 −x) = 0
⇐⇒ e= 0 (car x6= 1).
1

D’où e= 0 est un élément neutre. (1 pts)
v) Supposons que pour tout x∈R\ {1}, il existe x0∈R\ {1}tel que x∗x0= 0, alors :
x∗x0= 0 ⇐⇒ x+x0−xx0= 0
⇐⇒ x0(1 −x) = −x
⇐⇒ x0=x
x−1(car x6= 1).
D’où, tout x∈R\ {1}admet pour symétrique x0=x
x−1.(1 pts)
Conclusion : (R\ {1},∗)est un groupe abélien.
3- Soit f: (R∗,·)−→ (R\ {1},∗)l’application définie par f(x)=1−(1/x).
a) Montrer que fest un morphisme de groupes.
Soient x, y ∈R∗:
f(x)∗f(y) = 1−1
x∗1−1 y
=1−1
x+1−1 y−1−1 x1−1 y
= 1 −1
x+ 1 −1 y−1 + 1 x+1 y−1 xy
= 1 −1
xy
=f(x·y).
D’où fest un morphisme de groupes. (1,5 pts)
b) Calculer ker(f).
ker(f) = {x∈R∗:f(x)=0}
={x∈R∗: 1 −1
x= 0}
={x∈R∗:1= 1
x}
={x∈R∗:x= 1}
={1}.
D’où ker(f) = {1}.(1,5 pts)
c) Montrer que fest un isomorphisme de groupes.
i) D’après la question précédente on a ker(f) = {1}, on en déduit que fest un
morphisme injectif. (1 pts)
Montrons que fest surjectif. Soit y∈R\ {1}et supposons qu’il existe x∈R∗tel
que y=f(x):
y=f(x)⇐⇒ y= 1 −1
x
⇐⇒ 1
x= 1 −y
⇐⇒ 1 = x(1 −y)
⇐⇒ x=1
1−y.
2

D’où ∀y∈R\ {1},∃x∈R∗, x =1
1−y:y=f(x)et donc fest surjectif. (1,5 pts)
On en déduit que fest un morphisme bijectif (i.e., fest un isomorphisme). (0,5 pts)
II/ 1- Vérifier que pour tous x, y ∈R, on a : x∗y= 1 −(1 −x)(1 −y).
Soient x, y ∈R:
x∗y=x+y−xy
=x+y(1 −x)+1−1
=y(1 −x)−(1 −x)+1
= (1 −x)(y−1) + 1
= 1 −(1 −x)(1 −y).
D’où x∗y= 1 −(1 −x)(1 −y).(0,5 pts)
2- Pour tout entier n≥2et x∈R, évaluer la puissance nème :
x∗. . . ∗x
| {z }
nfois
.
Pour n= 2 on a : x∗x= 1 −(1 −x)2.
Pour n= 3 on a :
x∗(x∗x) = x∗[1 −(1 −x)2]
= 1 −(1 −x)h1−1−(1 −x)2i
= 1 −(1 −x)(1 −x)2
= 1 −(1 −x)3.
Montrons par récurrence qu’on a :
∀n≥2 : x∗. . . ∗x
| {z }
nfois
= 1 −(1 −x)n.(1 pts)
On a déjà vérifié que cette dernière équation est vraie pour n= 2. Supposons qu’elle est
vraie pour un entier n≥2et montrons qu’elle reste vraie pour n+ 1.(0,5 pts)
x∗. . . ∗x
| {z }
(n+1) fois
=x∗(x∗. . . ∗x)
| {z }
nfois
=x∗[1 −(1 −x)n]
= 1 −(1 −x)h1−1−(1 −x)ni
= 1 −(1 −x)(1 −x)n
= 1 −(1 −x)n+1.
D’où : ∀n≥2 : x∗. . . ∗x
| {z }
nfois
= 1 −(1 −x)n.(1 pts)
Exercice 2 : (6 pts)
On définit sur Zla relation Rpar :
∀n, m ∈Z, nRm⇐⇒ n+mest pair.
1. Montrer que Rest une relation d’équivalence.
3

(a) On a ∀n∈Z:n+n= 2n, et 2nest pair, donc ∀n∈Z:nRn. D’où Rest
reflexive. (0,5 pts)
(b) Soient n, m ∈Z:
nRm=⇒n+mest pair
=⇒m+nest pair
=⇒mRn.
D’où Rest symétrique. (0,5 pts)
(c) Soient n, m, r ∈Z:
nRm⇐⇒ n+mest pair
⇐⇒ ∃α∈Z:n+m= 2α
⇐⇒ ∃α∈Z:n= 2α−m.
mRr⇐⇒ m+rest pair
⇐⇒ ∃β∈Z:m+r= 2β
⇐⇒ ∃β∈Z:r= 2β−m.
d’où on obtient :
n+r= (2α−m) + (2β−m)
= 2α+ 2β−2m
= 2(α+β−m).
comme α+β−m∈Z, alors n+rest pair et donc (nRmet mRr) =⇒nRr),
c’est-à-dire que Rest transitive. (1,5 pts)
Conclusion : Rest une relation d’équivalence.
2. Calculer cl(0) et cl(1).
cl(0) = {n∈Z: 0Rn}
={n∈Z: 0 + nest pair}
={n∈Z:nest pair}
= 2Z.
D’où cl(0) = 2Z.(1 pts)
cl(1) = {n∈Z: 1Rn}
={n∈Z: 1 + nest pair}
={n∈Z:nest impair}
= 2Z+ 1.
D’où cl(1) = 2Z+ 1.(1 pts)
3. Vérifier que cl(0) et cl(1) forment une partition de Z.
(a) cl(0) = 2Z6=∅et cl(1) = 2Z+ 1 6=∅.(0,5 pts)
(b) cl(0) ∩cl(1) = 2Z∩(2Z+ 1) = ∅.(0,5 pts)
(c) cl(0) ∪cl(1) = 2Z∪(2Z+ 1) = Z.(0,5 pts)
Conclusion : cl(0) et cl(1) forment une partition de Z.
4