1ES3-coursDerivation.pdf (100.81 KB)

Dérivation
I Rappels sur les équations de droites
Soit ³O;−→ i;−→ j´un repère orthonormal.
Soit Dune droite.
Deux cas sont possibles :
•Dest parallèle à l’axe des ordonnées : tous les points de Dont la même abscisse k.
On dit alors que l’équation de Dest : x=k
•Dest sécante à l’axe des ordonnées.
Les coordonnées (x;y) des point de Dsont liées par une relation de la forme y=ax +b.
aet bsont caractéristiques de D:
*best appelé l’ordonnée à l’origine de D.
*aest le coefficient directeur de D.
best l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
O−→
i
−→
j
b
y=ax +b
amesure l’inclinaison de la droite.
•Si a>0, la fonction affine associée à la droite est crois-
sante.
•Si a=0, la fonction affine associée à la droite est
constante et la droite est parallèle à l’axe des ordon-
nées.
•Si a<0, la fonction affine associée à la droite est dé-
croissante.
O−→
i
−→
j
a>0
a<0
a=0
Plus précisément :
Page 1

Interprétation graphique du coefficient directeur :
O−→
i
−→
j
A
B
∆x
∆y
a=
∆y
∆x=yB−yA xB−xA
Comment utiliser le coefficient directeur pour tracer une droite ?
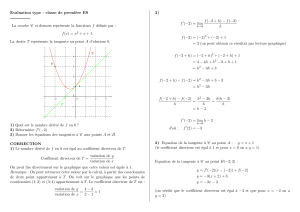
Exemple : Tracer la droite passant par le point A(2 ; 1) et de coefficient directeur égal à 3.
Nous avons vu que le coefficient directeur pouvait s’écrire ∆y
∆x.
Par conséquent : a=
∆y
∆x=3=3 1
Si l’on choisit de prendre ∆x=1, alors ∆y=3∆x=3×1=3. Par conséquent, en partant de A, l’on se déplace de
+1 unité en abscisses (donc de 1 unité vers la droite) et de +3 unités en ordonnées (donc de 3 unités vers le haut).
O−→
i
−→
j∆x=1
∆y=3×∆x=3
A
Si aest le coefficient directeur, on a : a=
∆y
∆xdonc ∆y=a×∆x; en choisissant une valeur pour ∆x, on calcule la
valeur correspondante pour ∆y.
Si, au lieu de prendre ∆x=1, on avait pris ∆y=2, on aurait trouvé ∆y=3×2=6 ; en partant de n’importe quel
point de la droite (A ou un autre), si l’on se déplace de 2 unités parallèlement à l’axe des abscisses, on se déplace
dans le même temps de 6 unités parallèlement à l’axe des ordonnées.
Page 2

II Taux de variation d’une fonction
Définition :
Le taux de variation d’une fonction fentre aet xest le nombre
f(x)−f(a)
x−a
En posant x=a+h, ce taux de variation s’écrit aussi f(a+h)−f(a)
h.
Interprétation graphique :
Soit fune fonction de courbe représentative C.
Notons Ale point de coordonnées (a;f(a)) (point fixe) et Mle point de coordonnées (a+h;f(a+h)) (point
variable).
Le taux de variation f(a+h)−f(a)
hde fentre aet a+hest le coefficient directeur de la sécante (AM) (droite
qui coupe Cen au moins deux points distincts,Aet M).
1
2
3
4
5
6
−1
−2
1 2 3 4−1−2−3−4
M
A
h
f(a+h)-f(a)
C
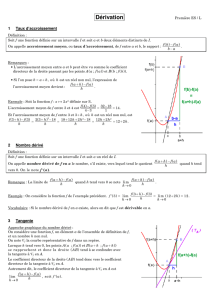
III Tangente à une courbe, nombre dérivé
Que se passe-t-il quand Arestant fixe, Mse rapproche de plus en plus de A.
La sécante (AM) se rapproche de plus en plus d’une droite limite, qui ne coupe plus la courbe Clocalement
qu’un point : on dit alors que cette droite « limite »est la tangente à Cen a(en pointillés sur le graphique ci-
dessous).
Page 3

1
2
3
4
5
6
−1
−2
1 2 3 4−1−2−3−4M
A
C
Ci-dessous est représentée la parabole, représentative de la fonction f:x7→ x2et les tangentes à Cen -2, -1, 0, 1
et 2,5.
1
2
3
4
5
6
7
8
9
−1
1 2−1−2−30
C
Définition :
Soit fune fonction définie sur un intervalle Iet soit A(a;f(a)) un point de la courbe Cf, représentative
de f.
Si Cfadmet une tangente en a, on appelle nombre dérivé de fen ale coefficient directeur de cette
tangente ; on le note f′(a).
Remarque :
On a vu que la tangente était la position limite d’une sécante (AM) lorsque le point variable Mse rapprochait de
plus en plus de M.
Le coefficient directeur de cette sécante est f(a+h)−f(a)
hoù a+het asont respectivement les abscisses de M
Page 4

et de A.
f′(a) est donc la limite, lorsqu’elle existe, de l’expression f(a+h)−f(a)
hlorsque hse rapproche de 0 en étant
différent de 0. (on dit « lorsque htend vers 0 »).
Cela s’écrit :
f′(a)=lim
h→0
f(a+h)−f(a)
h
Exemples de calculs de nombres dérivés :
•Fonction carré : f:x7→ x2.
(a) Cherchons le nombre dérivé f′(1), coefficient directeur de la tangente à Cfen 1.
Pour tout h6= 0, f(1 +h)−f(1)
h=(1+h)2−12 h=1+2h+h2−1 h=2h+h2 h=h(2+h) h=2+h.
Lorsque htend vers 0, le nombre 2+htend vers 2 : on écrit : lim
h→0
f(1+h)−f(1)
h=lim
h→0(2+h)=2.
On en déduit : f′(1) =2.
(b) Pour tout a, cherchons le nombre dérivé f′(a), coefficient directeur de la tangente à la parabole en a.
Pour tout h6= 0, f(a+h)−f(a)
h=(a+h)2−a2 h=a2+2ah +h2−a2 h=2ah +h2 h=h(2a+h) h=2a+h.
lim
h→0(2a+h)=0 donc lim h→0
f(a+h)−f(a)
h=2a.
On en déduit que, pour tout a:f′(a)=2a
•Soit fla fonction inverse : f:x7→ 1
x, définie sur R∗.
Soit a6=0.
f(a+h)−f(a)
h=
1
a+h−1 a
h=
a−(a+h)
a(a+h)
h=
−h
a(a+h)
h=− 1 a(a+h).
Lorsque htend vers 0, a+htend vers adonc a(a+h) tend vers a2.
On en déduit que : lim
h→0
f(a+h)−f(a)
h=lim
h→0
1
a(a+h)=− 1 a2.
On en déduit que : f′(a)=− 1
a2
•Soit la fonction racine carrée : f:x7→pxdéfinie sur [0 ; +∞[.
Pour tout a>0 et pour tout h6=0 :
f(a+h)−f(a)
h=pa+h−pa h=³pa+h−pa´×³pa+h+pa´
h׳pa+h+pa´=(pa+h)2−(pa)2 h³pa+h+pa´=a+h−a h³pa+h+pa´
=h
h³pa+h+pa´=1
pa+h+pa.
Lorsque htend vers 0, pa+htend vers padonc lim
h→³pa+h+pa´=pa+pa=2pa.
Par conséquent : lim
h→0
f(a+h)−f(a)
h=1
2pa
On en déduit que : f′(a)=2
2pa.
Page 5