11 Plan Fonctions vectorielles.pdf

Chapitre 11
Fonctions vectorielles
Dans tout le chapitre :  F désigne un -espace vectoriel de dimension finie.
 I désigne un intervalle de .
1. Dérivée en un point
1.1. Définition
 Fonction dérivable, vecteur dérivé
1.2. Interprétations
a) Existence d’un développement limité d’ordre 1 (caractérisation)
b) Interprétation graphique dans le cas où
F
c) Interprétation cinématique dans le cas où
2
F
. (resp.
n
)
 Notion de courbe paramétrée
 Le vecteur
0
ft
, lorsqu’il n’est pas nul, dirige la tangente en cet arc
au point
0
Mt
.
 Exemple : paramétrisation du cercle.
1.3. Extension : dérivée à droite, à gauche
2. Opérations sur les fonctions dérivables
2.1. Combinaisons linéaires
 Conservation du caractère dérivable par combinaisons linéaires.
 Traduction structurelle : structure de -espace vectoriel de
,IF
et
linéarité de l’opérateur D de dérivation.
2.2. Dérivation et linéarité
a) La propriété
 Si
,f I F
et
,L F G
,
,L f I G
et
L f a L f a
Démonstration
b) Application aux fonctions à valeurs dans
 Si
,fI
alors
,fI
,
Re ,fI
et
Im ,fI
et
ff
,
Re Reff
et
Im Imff
c) Raisonnement coordonnée par coordonnée

2.3. Dérivation et bilinéarité
a) La propriété
 Si
:B F G H
est bilinéaire,
,f I F
et
,g I G
,
alors
,,B f g I H
et
, = , ,B f g B f g B f g
Démonstration
b) Exemples : produit usuel, produit saclaire, produite vectoriel, déterminant,…
2.4. Dérivation et composition
 Si
:f I J
est en a et
:g J F
est dérivable en
()b f a
, alors
gf
est dérivable en a et
. ( )g f a f a g f a
Démonstration
3. Fonctions de classe k
3.1. Définition
3.2. Structures algébriques
3.3. Formule de Leibniz
Si
2
,,
n
f g I
alors
,
n
f g I
et
0
n
nn k k
k
n
f g f g
k
.
Démonstration
4. Intégration
4.1. Définition
4.2. Propriétés
a) Linéarité de l’intégrale
b) Relation de Chasles
c) Intégrale et norme
Soit
,,f a b F
. Alors
( ) ( )
bb
aa
f t dt f t dt
4.3. Sommes de Riemann
a) La propriété
Soient
,,f a b F
et
n
.
Soit
1
0
n
n
i
b a b a
S f a i
nn
une "somme de Riemann" de f sur
,ab
.
Alors la suite
nn
S
converge et
lim ( )
b
n
na
S f t dt
.
 Premier intérêt : convergence de la méthode des rectangles.

b) Son utilisation pratique
 Démontrer la convergence de certaines suites rebelles ; exemple.
4.4. Intégrale fonction de sa borne supérieure
a) La propriété
Théorème : Soit une fonction continue
:f I F
et
aI
.
Soit
:F I F
définie par
()
x
a
F x f t dt
.
Alors F est de classe
1
sur I et
Ff
.
De plus : F est l’unique primitive de f sur I qui s’annule en a.
Corollaire 1 : Toute fonction continue sur un intervalle admet des
primitives.
Ces primitives s’écrivent :
()
x
a
x k f t dt
où
kF
.
Corollaire 2 : Si F est une primitive de f sur
,ab
, alors
()
b
b
a
a
f t dt F b F a F t
.
  Une fonction non continue peut admettre des primitives.
  Une fonction continue par morceaux peut ne pas admettre de
primitive (avoir une idée du théorème de Darboux (H.P.)
 Savoir comment s’y prendre pour justifier la dérivabilité et dériver une
fonction du genre
()
()
( ) ( )
vx
ux
G x f t dt
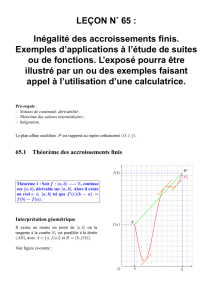
b) Inégalité des accroissements finis
Soit
1,f I F
et soit k est un majorant de
,,f t t a b
.
Alors
2
,a b I
:
( ) ( )f b f a k b a
Démonstration
 En particulier : Si
1,,f a b F
:
,
( ) ( ) ( )
t a b
f b f a Max f t
Corollaire : Soit
1,f I F
où I est un intervalle.
est constante sur 0 f I f
Démonstration

5. Particularités des fonctions à valeurs réelles (révisions de M.P.S.I.)
5.1. Dérivabilité et extremum
Théorème : Soit I un intervalle ouvert et
,fI
.
Si f admet sur I un extremum en a, alors nécessairement
0fa
.
 Conséquence : les extremums d’une fonction
,,f a b
sont
ou bien des bornes de l’intervalle
ou bien des points où la dérivée s’annule
  La réciproque du théorème est fausse
5.2. Théorème de Rolle
Théorème : Soit
, , , ,f a b a b
telle que
( ) ( )f a f b
.
Alors
, / 0ca b f c
.
5.3. Formule des accroissements finis
Théorème : Soit
, , , ,f a b a b
.
Alors
, / ( ) ( )ca b f b f a f c b a
.
Démonstration
5.4. Théorèmes de limite de la dérivée
a) Le lemme de base
Soit
,,f I I a
.
Si
lim
xa
fx
existe dans et est notée
alors
( ) ( )
lim
xa
f x f a
xa
existe et vaut .
b) Le théorème de limite de la dérivée
Théorème 1 : Soit
,,f I I a
.
Si
lim
xa
fx
existe dans : f est dérivable en a et
lim
xa
f a f x
Si
lim
xa
fx
: f n’est pas dérivable en a.
  Si
lim
af
n’existe pas dans , f peut poutant être dérivable en a
c) Théorème de prolongement du caractère 1
Théorème 2 : Soit
1
,,f I I a
.
Si
lim
xa
fx
existe dans , alors
1,fI
et donc
lim
xa
f a f x
.
 Prolongement au caractère k

5.5. Variations des fonctions et dérivation
5.6. Quant à l’intégration
a) Positivité, croissance
b) Précision : "positivité améliorée"
Propriété 3 : positivité améliorée (version 1)
Soit
,,f a b
.
S’il existe un point
0,tab
où
00tf
alors
( ) 0
b
a
f t dt
Propriété 4 : positivité améliorée (version 2)
Soit
,,f a b
. Si
( ) 0
b
a
f t dt
alors f est la fonction nulle.
5.7. Formules de Taylor
  Pour simplifier les choses, on suppose pour les lignes 1 à 4 du
tableau ci-dessous
1, n
fI
même si des hypothèses plus faibles
existent pour le théorème de Taylor-Young.
Pour la ligne 5 : f est une fonction polynôme de degré
n
.
Pour la ligne 6 : f est développable en série entière et
n
 On pose
1
, , ( ) ( ) !
k
n
k
n
k
ba
R f a b f b f a f a
k
Les diverses formules de Taylor
1
Taylor
avec reste intégral
,,
n
R f a b
1()
!
bn
n
a
btf t dt
n
2
Taylor-Lagrange
(inégalité)
1
, , . 1!
n
n
ba
R f a b K n
où
1
,
n
ab
K Sup f
3
Taylor-Lagrange
(comparaison)
1
,, n
n
R f a x O x a
4
Taylor-Young
,, n
n
R f a x o x a
5
Taylor
pour les polynômes
, , 0
n
R f a b
6
Développement
en série de Taylor
, , 0R f a b
 Application : développements limités
 Réviser les formules usuelles