Mouvement d’une balle de tennis Version adaptée

Mouvement d’une balle de tennis
Version adaptée
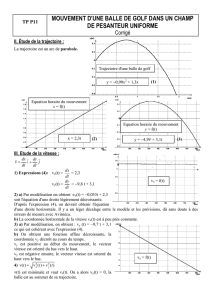
Un joueur de tennis tente de faire passer la balle au-dessus de son adversaire, situé à une distance d
derrière le filet. Il frappe la balle en O, à la distance D du filet et à la hauteur h au-dessus du sol.
La balle part avec une vitesse de valeur v
o
v
r0 = 14 m.s-1, inclinée d'un angle α = 60° par rapport au
milera la
sol horizontal.
. Dans ces
3)
Ovα
h
DdL
H
filet
La figure
n'est pas à
l'échelle. 1
balle à un point matériel et on négligera l'action de l'air. On prendra g = 10 m.s-2. On assi 1) Etablir, dans un repère que l'on définira, l'équation de la trajectoire de la balle.
2) L'adversaire, tenant sa raquette à bout de bras, peut atteindre la hauteur H
conditions, peut-il intercepter la balle ? H = 3,0 m ; d = 2,0 m ; D = 13,0 m et h = 0,5 m.
La distance de la ligne de fond à la base du filet étant L = 11,885 m 2, la balle peut-elle
éponses
retomber dans la surface de jeu ?
R
1°) Repère : origine en O, Ox horizontal dirigé vers le filet, Oz vertical dirigé vers le haut, Oy horizontal vers
système étudié : la n des forces : poids
l'arrière du plan de figure (Ox, Oy, Oz direct...).
balle M, dans le référentiel terrestre bila gmP
r
r
=
a
r
= ( 0, 0, - g ) v
r
= ( constante, constante, - g t + co ) = ( vo cosα , 0, - g t + v ) nstante o sinα
OM = ( vo cosα- ½ g t2 + vo sinα t ) y = 0 : trajectoire plane t , 0,
zgx
2
vxxx=− + =− +
2
022
201 17 cos tan , , α
α
2°) Pour x = D + d, zgD d
vDd m=−
+
++=
()
cos tan ( )
2
2
02
23 α
α ; alors que H - h = 2,5 m.
z > H - h : la balle ne peut pas être interceptée par l'adversaire.
3°) z = - h : −=− + =− +hgx
2
vxxx
2
022
201 17 cos tan , , α
α à résoudre
on choisit la solution positive : xv
g
v
g
v
ghm=+ +
2
04 022
2
2
02
21
cos sin cos sin cosαα α α α
=7
x < L + D = 24,885 m : la balle retombe dans la surface de jeu.
Version initiale
t que la figure n'est pas à l'échelle. Pas d'annotation indiquan
3) … L = 12 m….
1 Préciser la situation pour lever toute ambiguïté.
2 Utiliser une situation réaliste.
Académie de Créteil http://www.ac-creteil.fr/physique