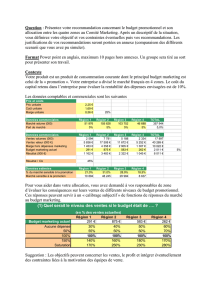
Cinématique en repères cylindrique et sphérique

Coordonnées cylindro-polaires (ou cylindriques)
Définition :
Oxyz : repère cartésien orthonormé direct
M : point quelconque
m : projeté orthogonal de M sur le plan Oxy
H : projeté orthogonal de M sur Oz
Ou : axe Om
r
u
: unitaire sur Ou
u
θ
: unitaire directement orthogonal à
r
u
dans
Oxy
z
u
: unitaire sur Oz
r = distance Om
θ =
angle(O ,O )
x u
z =
OH
OM
r z
ru zu
= +
vitesse de M : OM (M)
r
r z
d du
v ru r zu
dt dt
= = + +
ɺ
ɺ
or
r
u
est en rotation autour de
O
z
à la vitesse angulaire
θ
ɺ
, d’où
rz r
du
u u u
dt
θ
=θ × =θ
ɺ ɺ
, puis
(M)
r z
v r u r u z u
θ
= + θ +
ɺ
ɺ
ɺ
accélération de M :
(
)
M
(M)
r
r z
d v du d u
a r u r r u r u r z u
dt dt dt
θ
θ θ
= = + + θ + θ + θ +
ɺ ɺɺ ɺ
ɺɺ ɺ ɺ
ɺɺ
or
u
θ
est en rotation autour de
O
z
à la vitesse angulaire
θ
ɺ
, d’où
z r
du
u u u
dt
θθ
=θ × = −θ
ɺ ɺ
,
puis
(
)
(
)
2
(M) 2
r z
a r r u r r u z u
θ
= − θ + θ+ θ +
ɺ ɺ ɺɺ
ɺɺ ɺ
ɺɺ
déplacement élémentaire :
(
)
OM M
d v dt
= , d’où OM
r z
d dru rd u dzu
θ
= + θ +
surface élémentaire sur le cylindre d’axe Oz :
dS rd dz
= θ
volume élémentaire :
d rdrd dz
τ= θ
O
u
θ
x
y
r
u
θ
z
u
M
m
u
z
v
H

Coordonnées sphériques
Définition :
Oxyz : repère cartésien orthonormé direct
M : point quelconque
m : projeté orthogonal de M sur le plan Oxy
Ou : axe Om
OZ : axe OM
r
u
: unitaire sur OZ
u
θ
: unitaire directement orthogonal à
r
u
dans
OzZ
u
ϕ
: unitaire tel que
( , , )
r
u u u
θ ϕ
soit orthogonal
direct
r = distance OM
θ =
angle(O ,O )
z Z
ϕ =
angle(O ,O )
x u
OM
r
ru
=
vitesse de M : OM (M)
r
r
d du
v ru r
dt dt
= = +
ɺ
or
r
u
est en rotation autour de
O
z
à la vitesse angulaire
ϕ
ɺ
, et en rotation autour de
u
ϕ
à la
vitesse angulaire
θ
ɺ
, d’où
( )
sin
rz r
du
u u u u u
dt
ϕ θ ϕ
= θ +ϕ × = θ +ϕ θ
ɺ ɺ
ɺ ɺ
, puis
(M) sin
r
v r u r u r u
θ ϕ
= + θ + θϕ
ɺ
ɺ
ɺ
déplacement élémentaire :
(
)
OM M
d v dt
= , d’où OM sin
r
d dr u rd u r d u
θ ϕ
= + θ + θ ϕ
surface élémentaire sur la sphère de centre O :
2
sin
dS r d d
= θ θ ϕ
volume élémentaire :
2
sin
d r drd d
τ= θ θ ϕ
O
x
y
u
θ
ϕ
r
u
M
m
u
z
v
u
ϕ
H
θ
Z