Algèbre Géométrique Exercices corrigés Université de Paris 6

Algèbre Géométrique
Exercices corrigés
Université de Paris 6 Pierre et Marie Curie
Année 2006-2007
Niveau M1
Erwan Brugallé
[email protected]ssieu.fr

Table des matières
1 Actions de groupes 5
2 Espaces affines 15
3 Applications affines 31
4 Espaces projectifs 41
5 Espaces projectifs (suite) 49
6 Formes sesquilinéaires, symétriques et antisymétriques 61
7 Quadriques, isométries affines, algèbres de Lie 79
8 Algèbre multilinéaire 97

Chapitre 1
Actions de groupes
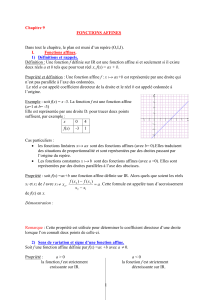
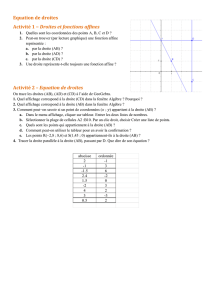
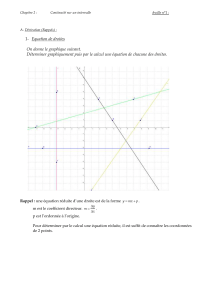
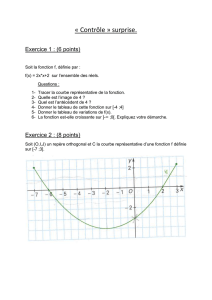
Exercice 1 (Définitions)
On rappelle qu’une action d’un groupe (G, ∗)sur un ensemble Eest la donnée d’un morphisme de
groupes Φ : (G, ∗)→(Bij(E),◦)de Gdans le groupe des bijections de E. On note en général
Φ(g)(x)par g·xou g(x). (Pour xdans Eet (g, g′)dans G2, calculer eG·xet (g∗g′)·x).
1. Donner un exemple d’action du groupe symétrique Sndes permutations d’un ensemble à n
éléments.
2. Donner un exemple d’action naturelle du groupe linéaire GL(V)d’un espace vectoriel Vsur
l’ensemble V.
3. Donner un exemple d’action de Zsur R.
4. Décrire les actions par translation à gauche, à droite et par automorphismes intérieurs d’un
groupe Gsur lui-même.
5. Décrire l’action naturelle du groupe symétrique Snsur l’ensemble des parties à péléments d’un
ensemble à néléments.
Corrigé : Puisque Φest un morphisme de groupe, on a Φ(eG) = Id (cad eG.x =x) et Φ(g∗g′) =
Φ(g)◦Φ(g′)(cad (g∗g′).x =g.(g′.x)).
1. Soit E={1,...,n}. Toute bijection de Eest une transposition, c’est à dire que le groupe Sn
est exactement le groupe des bijections de E. Donc Snagit naturellement sur Epar Φ(σ) = σ.
2. Le groupe GL(V)est un sous groupe de Bij(V). En effet, GL(V)est un sous ensemble de
Bij(V)stable par composition et par inversion. Donc comme dans la question précédente,
GL(V)agit naturellement sur Vpar Φ(f) = f.
3. Le groupe (Z,+) est un sous groupe de (R,+), donc Zagit naturellement sur Rpar translation
(voir question d’après), c’est à dire n.x =n+x(ou Φ(n)(x) = n+x).
4. Les trois actions sont données par
– translation à gauche : g.x =gx (ou Φ(g)(x) = gx)
– translation à droite : g.x =xg (ou Φ(g)(x) = xg)
– automorphisme intérieur : g.x =gxg−1(ou Φ(g)(x) = gxg−1)
5