integrales

Intégrales
I. D finitioné
a. D finitioné
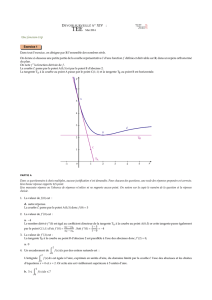
Soit f une fonction continue et positive sur . On pose E l'ensemble des points situés entre
et les droites d'équations et , alors est l'aire de E en unité d'aire.
b. Propri t s et remarquesé é
x et t sont des variables muettes.
Définition de l'aire E
E est l'ensemble des points tels que
Propriété
Toute fonction continue sur I est intégrable sur I.
La réciproque est en revanche fausse.
Exemple :
Pourtant, il s'agit d'une fonction discontinue
[a;b]
Cf; (O
x
)
x=a
x=b
Z
b
a
f(x):dx
Z
b
a
f(x):dx =Z
b
a
f(t):dt
M(x;y)
a6x6b
06y6f(x)
Z
2;5
0
Int(x):dx = 2

Signe de l'intégrale
Le signe de l'intégrale est le signe de la fonction intégrée
Signe de l'aire
Si f est positive, aire de E
Si f est négative, aire de E
Fonction constante
Soit f une fonction constante sur , alors
Relation De Chasles
aire de E + aire de E' aire de
Soit f une fonction continue sur un intervalle I et a, b et c I, on a la relation de Chasles :
Z
a
a
f(x):dx = 0
Z
b
a
f(x):dx =
Z
b
a
f(x):dx =¡
=
(E[E
0
)
=Z
b
a
f(x):dx +Z
c
b
f(x):dx =Z
c
a
f(x):dx
2
Z
b
a
f(x):dx +Z
c
b
f(x):dx =Z
c
a
f(x):dx
k(k > 0) [a;b]
Z
b
a
k:dx =k(b¡a)

Bilinéarité
Soient f et g deux fonctions continues sur
, avec
Int grale et ordreé
Si f et g sont continues [a;b] et ,
alors
Aire entre les deux courbes
Si f et g sont continues sur et ,
alors l'aire comprise entre Cf et Cg est égale à
Démonstration
Aire de
Valeur moyenne
Soit une fonction continue sur [a;b] . La valeur moyenne de f sur [a;b] est
Z
b
a
f(x):dx =¡Z
b
a
f(x):dx
[a;b]
Z
b
a
(f(x) + g(x)):dx =Z
b
a
f(x):dx +Z
b
a
g(x):dx
Z
b
a
k:f(x):dx =kZ
b
a
f(x):dx
k2R
Z
b
a
(k:f(x) + k
0
:g(x)):dx =kZ
b
a
f(x):dx +k
0
Z
b
a
g(x):dx
8
x
2[a;b] f(x)6g(x)
Z
b
a
f(x):dx 6Z
b
a
g(x):dx
Z
b
a
g(x):dx ¡Z
b
a
f(x):dx =Z
b
a
(g(x)¡f(x)):dx
[a;b] 8
x
2[a;b] f(x)6g(x)
Z
b
a
(g(x)¡f(x)):dx
f606g
E
1
[E
2
=E
1
+E
2
Z
b
a
g(x):dx ¡Z
b
a
f(x):dx =Z
b
a
(g(x)¡f(x)):dx
f6g60
Z
b
a
f(x):dx ¡Z
b
a
¡g(x):dx =Z
b
a
(g(x)¡f(x)):dx
A=1
b¡a£Z
b
a
f(x):dx

L'aire du rectangle est égale à l'aire du trapèze.
Inégalité de la moyenne
Soit une fonction continue sur [a;b]. Si , alors
Démonstration
f paire et
Par symétrie,
D'après la relation de Chasles,
f impaire et continue sur
L'aire de est égale à l'aire de
d'où
Exemple :
f est continue sur et impaire
8
x
2[a;b]; m < f (x)< M
¸2[a;b]
8
x
2[a;b]; m < f (x)< M
a > 0
Z
0
¡a
f(x):dx =Z
a
0
f(x):dx
Z
a
¡a
f(x):dx = 2 Z
a
0
f(x):dx
[¡a;a]
E
1
E
2
Z
a
¡a
f(x):dx =Z
0
¡a
f(x):dx +Z
a
0
f(x):dx = 0
Z
¼
4
¡¼
4
f(x) = tan
3
(x)
(3 + sin
2
(x))
15
:dx
f(¡x) = tan
3
(¡x)
(3 + sin
2
(¡x))
15
=¡tan
3
(x)
(3 + sin
2
(x))
15
=¡f(x)
[¡¼
4;¼ 4]
,Z
b
a
m:dx 6Z
b
a
f(x):dx 6Z
b
a
M:dx ,m(b¡a)6Z
b
a
f(x):dx 6M(b¡a)
Z
0
¡a
f(x):dx =¡Z
a
0
f(x):dx
m61
b¡a£Z
b
a
f(x):dx 6M() m(b¡a)6Z
b
a
f(x):dx 6M(b¡a)

II. Primitives
Fonction Primitive
Fonction Primitive
Lien entre intégrale et primitive
Soit une fonction f continue sur I avec , alors est la primitive de f qui
s'annule en a.
a2I
F(x) = Z
x
a
f(t):dt
x
n+1
n+ 1
ax
a
x
n
1
x
n
¡1
(n¡1)x
n¡1
2px
1
px
cos(ax +b)
¡1
acos(ax +b)
1
asin(ax +b)
sin(ax +b)
u
0
e
u
e
u
u
0
u
ln(u)
u
0
u
n
¡1
(n¡1)u
n¡1
2pu
u
0
pu