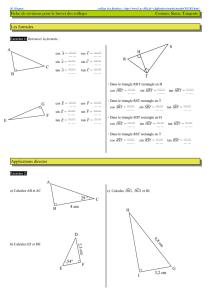
Correction du devoir maison n°5

4) a) Calculer la mesure de l’angle
On sait que
le triangle COA est rectangle en C
Donc
on a cos 
 =
cos 
 =
donc = 60°
Correction du devoir maison n°5
Ex 56 p 242
1) On sait que dans le triangle AOC rectangle en C,
D’après le théorème de Pythagore, on a
AO² = AC² +CO²
AC² = AO² - OC²
AC² = 6² -3²
AC² = 36 – 9
AC² = 27 or AC > 0
AC =
AC =   
AC = 3 cm
2) On sait que le triangle ENO est rectangle en E et le triangle CAO est rectangle en C
donc (NE)  (EO) et (AC)  (OC)
De plus les points E, O et C sont alignés donc les droites (EO), (EC) et (OC) sont confondues
Le point S appartient à la droite (NE) donc les droites (NS ) et (NE) sont confondues
Propriété : Si deux droites sont perpendiculaires à une même droite
alors ces deux droites sont parallèles
Donc (NS) // (AC).
b) Calculer les valeurs exactes de ES et de OS
 On sait que dans les triangles OES et OCA,
 Les droites (AS) et (EC) sont sécantes en O.
 (ES) // (AC)
D’après le théorème de Thalès, on a :
OE OS ES
OC OA AC
= =
donc :
5
3 6
3 3
OS ES
= =
5 5 6
:
6 3
10
3
OS
Calcul de OS don
m
c OS
c
×
= = =
5 5 3 3
:35 3
3
3 3
ES
Calcul de ES don
cm
c ES × = = =
3) Calculer la EN
On sait que le triangle NOE est rectangle en E
Donc on a tan =
tan =
NE = 5 x tan 30°
NE ≈ 2,9 cm (arrondi au mm)
b) Démontrer que le triangle est rectangle
Les angles et sont opposés par le sommet
Donc ils ont la même mesure
=60°
= +
= 30 + 60
 = 90° donc le triangle NOS est rectangle en O
A
C

3 20 45
3 4 5 9 5
3 4 5 9 5
3 2 5 3 5
5
9
6 5 3
5
A
A
A
A
A
A
= +
= × + ×
= × × + ×
= ×
+
=
+
=
180 3 5
9 2 2 5 3 5
9 4 5 3 5
3 2 5 3 5
6 5 3 5
3 5
B
B
B
B
B
B
= −
= × × × −
= × ×
× −
= −
=
−
=
9 5 3 5
9 3 ( 5)
2
35
5
1
²
7
A B
A B
A B
A B
donc A B est un nombre entier
×
× = ×
× = ×
×
×
× = ×
=
9 5
3 5
3
3
9
A A
donc est un nombre entier
B B
A
B
A
B
=
=
=
sin 60
tan 60
cos 60
3
2
tan 60 1
2
3 2
tan 60
tan 0 3
1
6
2
=
=
=
=
×
(cos 60)² (sin 60)² 1
(sin 60)² 1 (cos 60)²
1
(sin 60)² 1 ( )²
2
4 1
(sin 60)² 4 4
3
(sin 60)² 4
3
sin 60 4
3
sin 60
2
+ =
= −
= −
=
=
=
−
=
(cos 30)² (sin 30)² 1
(cos 30)² 1 (sin 30)²
1
(cos 30)² 1 ( )²
2
4 1
(cos 30)² 4 4
3
(cos 30)² 4
3
cos30 4
3
cos30
2
+ =
= −
= −
=
=
=
−
=
sin 30
tan 30
cos30
1
2
tan 30 3
2
1 2
tan 30 2
3
1
tan 3
3
tan
0
30
3
3
=
=
=
=
×
=
Ex 77p 80
2°) Démont rer que A×B et sont des nombre entiers
1°)
Ex 69 p 244
2°) Dans un triangle équilatéral, les trois angles sont égaux et valent 60°
Donc 
 = 60°
On sait que (AH) est la hauteur issue de A dans le triangle ABC
Donc le triangle ABH est rectangle en H
Dans un triangle rectangle, les angles aigus sont complémentaires
Donc  = 90 – 60
 = 30°
3 °) a) On sait que dans le triangle ABH rectangle en H
Donc on a cos =
cos =
on sait que le triangle ABC est équilatéral donc la hauteur (AH) est aussi la médiatrice de [BC]
donc H est le milieu de [BC] et BH
En particulier et cos  =
3 °) a) On sait que dans le triangle ABH rectangle en H
Donc on a sin =
sin  =
b)
A
C B
60°
30°