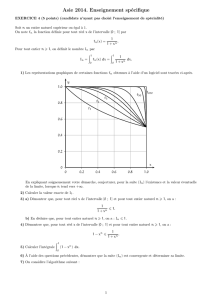
Télécharger

I
I
I
R C
f: [a, b[→R C b6+∞
Zb
a
f(t)tZx
a
f(t)t x b [a, b[
Zb
a
f(t)t= lim
x→bZx
a
f(t)t
O
Cf
x→b a

Zb
a
f(t)t
Z]0,1]
t
√t
Z+∞
1
t
tα⇐⇒ α > 1
Z1
0
t
tα⇐⇒ α < 1
Z+∞
0
e−at t⇐⇒ a > 0
Z1
0
ln t t =−1
α > 1
Z+∞
1
t
tα=1 α−1
O
t7→ 1
tα(α > 1)
x→+∞
1
α < 1
Z1
0
t
tα=1 1−α
H
N
x→0x7→ Z1
x
t
tα
? α 6= 1 Z1
x
t
tα=1 (1 −α)tα−11
x
=1
1−α−1 (1 −α)xα−1
α > 1 +∞x0
α < 11
1−αx0

? α = 1
Z1
x
t
t=ln(t)1
x=−ln(x)−→
x→0+∞
0
t7→ 1
tα(0 <α<1)
←x1
a > 0
Z+∞
0
e−at t=1
a
t7→ ln t]0,+∞[
Zb
a
t
(t−a)α⇐⇒ α < 1
Zb
a
t
(b−t)α⇐⇒ α < 1
a)Z1
0
t
3
√tb)Z+∞
0
2−tt c)Z2
1
t
√t−1

f∈ C([a, b[,C)c∈[a, b[
Zb
a
f(t)t⇐⇒ Zb
c
f(t)t
Zb
a
f(t)t=Zc
a
f(t)t+Zb
c
f(t)t
f, g ∈ C([a, b[,C)λ, µ ∈C
Zb
a
f(t)tZb
a
g(t)tZb
a
(λf +µg)(t)t
Zb
a
(λf +µg)(t)t=λZb
a
f(t)t+µZb
a
g(t)t
Z+∞
2
2t
t2−1=Z+∞
2
t
t−1−Z+∞
2
t
t+ 1
x > 2
Zx
2
2t
t2−1=Zx
2
t
t−1−Zx
2
t
t+ 1 = ln h3x−1 x+ 1i−→
x→+∞ln 3
f∈ C([a, b[,C)f=f1+if2f1∈ C([a, b[,R)f2∈ C([a, b[,R)
Zb
a
f(t)t⇐⇒ Zb
a
f1(t)tZb
a
f2(t)t
Zb
a
f(t)t=Zb
a
f1(t)t+iZb
a
f2(t)t
`
` x b x 7→ Zx
a
f(t)t
x7→ Zx
a
f1(t)t x 7→ Zx
a
f2(t)t
[a, b[f[a, b[`
b f b f
(b
f(t) = f(t)t∈[a, b[
b
f(b) = `

Zb
a
f(t)tZ[a,b]b f
[a, b[f[a, b]b f
Z1
0
sin t
ttZ[0,1]
sin t
tt
t7→ sin t
tt= 0
lim
x→b
x<b
Zx
a
f(t)t= lim
x→b
x<b
Zx
ab
f(t)t=Zb
ab
f(t)t
fb f[a, b[ [a, b]
x7→ Zx
ab
f(t)tb f
f∈ C(]a, b[,C)a, b ∈¯ RZb
a
f(t)t c ∈]a, b[Zc
a
f(t)tZb
c
f(t)t
Zb
a
f(t)t=Zc
a
f(t)t+Zb
c
f(t)t
Z+∞
−∞
t
1 + t2
f−f
f∈ C([a, b[,R+)M > 0
∀x∈[a, b[,Zx
a
f(t)t6MZb
a
f(t)t
x7→ Zx
a
f(t)t[a, b[b
x7→ Zb
x
f(t)t]a, b]
a