énergie - Physique PCSI1 Lycée Michelet

PCSI1Lycée Michelet
ÉNERGIE
1
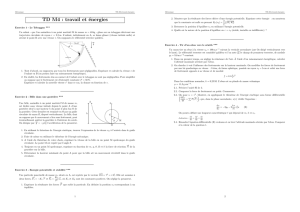
On représente la trajectoire d’un objet jeté en l’air. On note vla norme
de son vecteur vitesse et on compare vaux points A,Bet C(Aet C
étant situés sur une même horizontale). Quelle est la bonne proposition ?
On justifiera soigneusement sa réponse.
(a)vA> vB> vC(c)vA=vC> vB
(b)vA> vC> vB(d)vC> vA> vB
2 Distance de freinage
Calculer la distance Dde freinage d’une voiture lancée à la vitesse v0sur
une route horizontale (µcoefficient de frottement solide entre les roues et
la route). On néglige les frottements de l’air.
Application numérique :v0= 40 m.s−1,g= 10 m.s−2,µ= 0,6(route
sèche), puis µ= 0,2(route mouillée).
Réponses : D= 133 m ; D= 400 m.
3 Toboggan
Un adulte (m= 70 kg) descend un toboggan d’une hauteur h= 5,0m
faisant un angle α= 45◦avec le sol. En présence de frottements solide, la
norme de la composante tangentielle −→ RTde la réaction −→ Rest donnée par
k−→ RTk=fk−→ RNkoù fest le coefficient de frottement (f= 0,4) et −→ RNest
la composante normale de la réaction. On prendra g= 9,8m.s−2.
1) Vérifier que l’angle αest suffisamment élevé pour que le glissement
puisse avoir lieu.
2) Calculer la variation de l’énergie mécanique due au frottement entre le
haut et le bas du toboggan.
3) Déterminer la vitesse de la personne en bas du toboggan. La comparer
à celle qu’elle aurait s’il n’y avait pas de frottement.
Réponses : avec frottements v= 7,7m.s−1;
sans frottement v= 9,9m.s−1.
4
Une balle tombe d’une hauteur ho= 1 m sur un plancher sur lequel elle
rebondit. Elle repart vers le haut avec une vitesse v1=evo,voétant
la vitesse de la balle lorsqu’elle atteint le plancher. Le coefficient de
restitution eest égal à 0,8. On négligera les frottements de l’air.
Quelles sont les hauteurs h1,h2.. et hnatteintes par la balle après le
premier rebond, le second.. le nieme ?
5 Limites de trajectoire et énergie
Une particule fixe, de charge électrique qest placée à l’origine Od’un axe
Ox (problème à une dimension axiale). On néglige le poids des particules.
1) On lance à une distance ade Oune seconde particule, de charge −qet
de masse m, dans une direction tendant à l’éloigner de O. Quelle vitesse
initiale v0doit-on lui communiquer pour qu’elle échappe à l’attraction de
la particule fixe placée en O? On pourra justifier sa réponse à l’aide d’un
graphique énergétique.
2) La particule mobile a maintenant la charge +qet sa vitesse initiale est
dirigée vers O. Montrer que cette particule ne peut atteindre O; calculer
la distance minimale d’approche ben fonction de v0.
D’après vous, dans quel but cherche-t-on a rapprocher deux charges posi-
tives ?
1

PCSI1Lycée Michelet
6 Mouvement d’une bille sur un support
Une bille de masse mest déposée à une hauteur hsur un support, dont
la seconde partie est circulaire de rayon R=h/2. Aucun frottement n’est
envisagé.
a) Quelle sera la vitesse maximale atteinte par la bille ?
b) Déterminer l’expression de la réaction normale ~ Ndu support en fonc-
tion de θ.
c) En déduire pour quelle valeur de l’angle θla bille décolle.
7 Détermination de positions d’équilibre. Étude
de leur stabilité
O
M
A
x
a
On considère le système représenté sur la
figure ci-contre. La masse mglisse sans
frottement le long de l’axe Ox. Elle est
attachée à un ressort de longueur à vide
lo, de raideur k, fixé en Ad’abscisse a.
1) Montrer que le mouvement est conser-
vatif et exprimer Ep(x), l’énergie poten-
tielle de la masse mà une constante ad-
ditive près.
2) En déduire les positions d’équilibre possibles. On distinguera les trois
cas suivant :
–a<lo
–a=lo
–a>lo
3) Étudier la stabilité des positions d’équilibre déterminées précédemment.
4) Déterminer la période des petites oscillations au voisinage des positions
d’équilibre stables dans le cas où a<loet a > lo.
5) On se place dans le cas a=lo. Établir l’équation des oscilla-
tions au voisinage de la position d’équilibre stable. Montrer que l’on
n’obtient plus d’oscillations harmoniques. On note T, la période des os-
cillations et x0leur amplitude. Établir une relation intégrale entre Tet x0.
Il pourra être utile pour faire cet exercice de consulter le site :
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/
Meca/Oscillateurs/ressort_bifur.html
2

PCSI1Lycée Michelet
8 Éruption volcanique sur Io.
A - Préambule
A.1. On considère la force de pesanteur m~g =−mg ~ez. Déterminer l’ex-
pression de l’énergie potentielle dont dérive cette force, à une constante
additive près. Déterminer cette constante dans le cas particulier où on
choisit Ep= 0 en z= 0.
A.2. On considère un point matériel Mde masse m, placé dans le champ
gravitationnel d’un astre à symétrie sphérique de masse M0et de centre O.
On admettra que cet astre est assimilable à un point confondu avec son
centre Oet de masse M0. On note −−→ OM =r ~er.
A.2.a. Donner l’expression de la force gravitationnelle ~ Fqui s’exerce sur
la masse men coordonnées sphériques, en fonction de m,M0,Gconstante
gravitationnelle, ret ~ervecteur unitaire des coordonnées sphériques.
A.2.b. Rappeler l’expression du déplacement élémentaire d−−→ OM en coor-
données sphériques. En déduire l’expression du travail élémentaire de la
force ~ F.
A.2.c. Déterminer l’expression de l’énergie potentielle dont dérive ~ F, à
une constante additive près. On choisit Epnulle à l’infini. En déduire la
valeur de la constante.
B - Étude du panache volcanique
À partir des données envoyées par l’engin spatial Voyager 1 en 1979, l’ingénieure
Linda Morabito a découvert sur Io, un des satellites de Jupiter, la première ac-
tivité volcanique extra-terrestre. Le panache de l’éruption s’élevait à une altitude
h= 280 km environ (on considèrera que cette donnée comporte deux chiffres
significatifs). Io ne possède quasiment pas d’atmosphère, on négligera donc toute
force de frottement. On suppose le référentiel lié à Io (i.e dans lequel Io est fixe)
galiliéen.
B.1. Sachant que le champ de pesanteur à la surface de Io vaut g0= 1,8
m.s−2et en supposant qu’il reste constant sur toute la hauteur du pa-
nache, déterminer la vitesse và laquelle les débris étaient projetés de la
surface de Io. On exprimera tout d’abord ven fonction de g0et hpuis on
fera l’application numérique.
B.2. Io est un satellite de forme sphérique, de masse M0, de rayon
R0= 1,82.103km. Il pourra être assimilé à une masse ponctuelle M0pla-
cée en son centre. On rappelle que champ de pesanteur ~g est lié à la force
gravitationnelle ~ Fs’exerçant sur une masse mpar la relation ~ F=m~g.
B.2.a. On note ~g0=−g0~erle champ gravitationnel à la surface de Io.
Exprimer g0en fonction de Gconstante gravitationnelle, M0et R0.
B.2.b. On note ~g =−g ~erle champ gravitationnel à l’altitude h. Exprimer
gen fonction de G,M0,R0et h, puis en fonction de g0,R0et h. Calculer
le rapport g
g0
.
B.2.c. Que pensez-vous de l’approximation faite au 1. ? A-t-elle conduit à
surestimer ou à sous-estimer la vitesse d’éjection des débris ? On fournira
une réponse argumentée, mais ne comportant pas de calcul.
B.3. On tient désormais compte de la variation de gavec l’altitude.
En utilisant une méthode énergétique, déterminer la vitesse v0d’éjec-
tion des débris à la surface de Io. On exprimera v0en fonction de G,
M0,R0et hpuis en fonction de g0,R0et h. Faire l’application numérique.
3