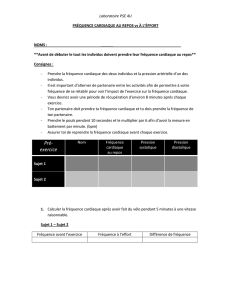
Résultat Soit ∑ ak une série à termes réels ou complexes

1/17
Séries
Séries de puissances
Critère de la racine
Critère des séries alternées
Résultat
Soit Pakune série à termes réels ou complexes. Supposons que la limite
limk→∞
k
p|ak|existe et vaut L, éventuellement L = +∞. Alors
si L <1, la série converge absolument ;
si L >1, la série diverge ;
(si L =1, le test ne conclut pas).
Démonstration.
Si L>1, alors |ak|>1 à partir d’un certain rang, et donc ne peut pas
tendre vers 0, ce qui implique la divergence de la série.
Si L<1, alors pour t=L+1
2, on a |ak|<tkà partir d’un certain rang. Le
critère de comparaison avec la série géométrique s’applique alors puisque
t<1 : Pktkconverge, donc Pkakconverge également.

2/17
Séries
Séries de puissances
Critère de la racine
Critère des séries alternées
Définition
Une série alternée est une série Pjcjtelle que cj+1et cjont des signes
distincts (l’un négatif, l’autre positif) pour tout j(à partir d’un certain
rang.)
Exemple
Les séries suivantes sont des séries alternées :
X
k
(−1)k,X
k
(−1)k
k,X
k
(−1)k
k2,X
k
(−k)k

3/17
Séries
Séries de puissances
Critère de la racine
Critère des séries alternées
Résultat
Si Pjcjest une série alternée telle que la suite (|cj|)
est décroissante (à partir d’un certain rang), et
tend vers 0
alors la série converge.
Exemple
La série harmonique alternée Pk
(−1)k
kest convergente (mais ne converge
pas absolument).

4/17
Séries
Séries de puissances
Critère de la racine
Critère des séries alternées
La preuve est omise, mais un petit dessin suffira à nous convaincre :
sjj
abcisses : les valeurs de k,
ordonnées : les valeurs de sk, la k-ième somme partielle.

5/17
Séries
Séries de puissances
Le rayon de convergence
Théorème de dérivation d’une série de puissances
Rappelons que le polynôme (ou développement) de Taylor d’ordre nd’une
fonction fautour d’un point aprend la forme suivante :
Tf,a,n(x) =
n
X
k=0
fk(a)(x−a)k
k!
=f(a) + f0(a)(x−a) + f00(a)(x−a)2
2+· · · +fn(a)(x−a)n n!.
Cette formule fait penser à une somme partielle d’une série.
Définition
Si f:A⊂R→Rest de classe C∞, et aest intérieur à A, alors la série de
Taylor de fen aest la série :
∞
X
k=0
fk(a)(x−a)k
k!.