Probabilités sur un univers dénombrable

(An)n∈N
(Ω, P )
lim
n→+∞P(An)=0.
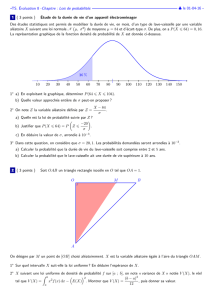
6
3
1/4
1
n
n
0,95
p1>0
p2>0
p1p2
2/3
X
pn=P(X=n)
p2, p3p4
n∈N∗
pn+2 =1
3pn+1 +2 9pn.
pnn∈N∗
n∈N∗
X
P(X>k)k∈J1, nK
X
X
X
X
p∈]0,1[ 1/X
X
λ > 0 1/(X+ 1)

X P
P X
X
P
a∈RXN∗
∀n∈N∗, P (X=n) = a
n(n+ 1).
a
X
a∈RXN∗
∀n∈N∗, P (X=n) = a
n(n+ 1)(n+ 2).
a
X
N N
λ > 0n∈N(N=n)
X n p ∈]0,1[
X
p∈]0,1[
p
X
X
X
X
NX
(m, n)∈N2
P(X > m)>0P(X > m +n|X > m) = P(X > n).
p∈]0,1[
P(X > 0) = 1
m∈N
P(X > m + 1) = P(X > 1)P(X > m).
X
X X
a > 0X
X X 2
X X = 0 p
q
p+q p −q p q