Relations trigonométriques dans les triangles rectangles On ne

Relations trigonométriques dans les triangles rectangles
On ne considère dans ce chapitre que des triangles rectangles.
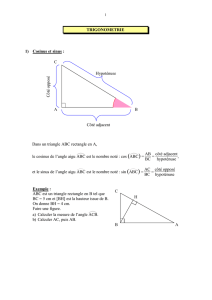
Côté adjacent à
ABC
Côté opposé à
ABC
Hypoténuse
La notion de côté opposé et de côté adjacent dépend de l'angle considéré, contrairement à l'hypoténuse
d'un triangle rectangle.
1- Cosinus d'un angle aigu
Adjacent
Définition :
cos ABC
=
AB
BC
Hypoténuse
Remarque :
cos ACB=AC
BC
Exemple 1 Le triangle EFG est rectangle en G.
cos GEF =EG
EF
cos GEF =7
9
A la calculatrice, on en déduit une valeur approchée
de la mesure de l'angle :
EFG≈38,9 °
2- Sinus d'un angle aigu
Opposé
Définition :
sin ABC
=
AC
BC
Hypoténuse
Remarques :
sin ACB=AB
BC
sin ACB=cos ABC
Exemple 2 Le triangle MAD est rectangle en A.
sin MDA=MA
MD
sin MDA=5
13
A la calculatrice, on en déduit une valeur approchée
de la mesure de l'angle :
MDA≈22,6 °

3- Tangente d'un angle aigu
Opposé
Définition :
tan ABC
=
AC
AB
Adjacent
Remarques : ●
tan ABC=sin
ABC
cos ABC
Démonstration :
sin ABC
cos ABC =
AC
BC
AB
BC
=AC
BC ×BC AB =AC AB =tan
ABC
● tan 90° n'existe pas !
Exemple 3 Le triangle HNB est rectangle en N.
tan HBN=NH
NB
tan HBN =2
9
A la calculatrice, on en déduit une valeur approchée
de la mesure de l'angle :
HBN ≈12,5 °
Moyen mnémotechnique pour se souvenir de ces formules :
Sinus
Opposé
Hypoténuse
Cosinus
Adjacent
Hypoténuse
Tangente
Opposé
Adjacent
Exemple 4 : calcul de la longueur du côté d'un triangle
Je sais que le triangle ABC est rectangle en A.
tan ABC=AC
AB
tan 32 °
1=7 AB
AB=7×1
tan 32 °
AB≈11,2
AB mesure environ 11,2 cm.
A
B
C
32°
7 cm

4- Propriété fondamentale
Quel que soit l'angle x, on a :
cos x
2
sin x
2=1
Ce qui s'écrit aussi :
cos2xsin2x=1
Démonstration :
Je sais que le triangle ABC est rectangle en A.
cos ABC=BA
BC
sin ABC=AC
BC
cos ABC
2
sin ABC
2=
BA
BC
2
AC
BC
2
=BA2
BC2AC2 BC2=BA2AC2 BC2
Or, d'après le théorème de Pythagore, on a :
BA2AC2=BC2
On en déduit que :
cos ABC
2
sin ABC
2=BC2
BC2=1
D'où la formule.
Remarques : ● Dans un triangle rectangle (angle x aigu), on a toujours :
0 ≤ cos x ≤ 1
0 ≤ sin x ≤ 1
0 ≤ tan x
● Le cosinus, le sinus et la tangente d'un angle sont des nombres sans unité.
● Ces formules permettent soit de calculer la mesure d'un angle, soit de calculer la
longueur d'un segment.
● A chaque valeur d'angle aigu correspond une seule valeur du cosinus, du sinus et de la
tangente et réciproquement.
A
B
C
32°
7 cm