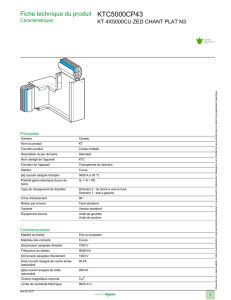
Solution Diophante-Pantaloni-D626

D626.Une bien étrange figure . . .
Vincent PANTALONI
30 janvier 2010
Enoncé : Construire la figure ci-dessous où les segments de même couleur sont de même
longueur.
Solution : .........................................................................................
La construction à la règle et au compas sans calcul, s’avère contre toute attente impossible (à
mon avis), il y a un paramètre manquant (angle ou longueur) qu’on ne parvient à ajuster. C’est en
cherchant une solution au cas n= 7 du problème D249
http://www.diophante.fr/Problemes-ouverts/D249.-Le-casse-tete-d-Erdos-et-ses-variantes.html
que je me suis intéressé à cette figure et ai essayé longtemps mais en vain de la construire. J’ai du
faire des calculs pour déterminer le cosinus d’un des angles de la figure.
1 Relations entre les angles.
On raisonne par analyse-synthèse. Supposons donc la figure construite, on peut la voir comme un
pavage fait avec deux triangles isocèles de côtés oranges (noté l) et bleus (noté L).
Remarque :
J’ai d’abord cru qu’il s’agissaient des deux triangles d’Or qui apparaissent dans le pavage de Penrose
http://fr.wikipedia.org/wiki/Pavage_de_Penrose#Pavage_de_Penrose_avec_triangles_d.27or_.28pavage_de_type_0.29
Mais en fait, non. Cependant on verra un lien au bout des calculs.
On code les angles comme sur les figures ci-dessous.
I
ODEG
K
J
C
O
L
l
α
β
a
b
1

http://www.diophante.fr/ D626
On a les relations suivantes entre les angles :
a+ 2α= 180 (1)
b+ 2β= 180 (2)
β+α= 2 ×2α(3)
Les deux premières viennent de la somme des angles dans chacun des deux triangles isocèles.
La (3) est la traduction de l’angle au centre Odu cercle Cqui vaut le double de l’angle au sommet I:
\
JOK = 2
[
JIK
La (3) fournit β= 3α, on en déduit tous les angles en fonction de α:
a= 180 −2α(4)
b= 180 −2β= 180 −6α(5)
β= 3α(6)
Pour tenir compte des longueurs oranges et bleues, j’ai appliqué la relation dite d’Al–Kashi dans
chacun des triangles isocèles :
L2= 2l2−2l2cos a(7)
l2= 2L2−2L2cos b(8)
En utilisant les relations (4) et (5) ainsi que la formule cos(180 −x) = −cos(x)on obtient :
L2= 2l2(1 + cos 2α)(9)
l2= 2L2(1 + cos 6α)(10)
On pose comme inconnue x= 2α, et en remplaçant l2par son expression en (10) dans la précédente,
on obtient :
L2= 2 ×2L2(1 + cos 3x)(1 + cos x)
D’où en simplifiant par L2:
4(1 + cos 3x)(1 + cos x)−1 = 0
Or cos(3x) = 4 cos(x)3−3 cos(x). En remplaçant, développant et simplifiant on obtient cette équation
de degré 4 en cos(x):
16 cos(x)4+ 16 cos(x)3−12 cos(x)2−8 cos(x) + 3 = 0 (11)
2 Équation de degré 4
Ainsi cos(x)est solution de l’équation de degré 4 :
16X4+ 16X3−12X2−8X+ 3 = 0 (12)
Xcas avec solve(16X4+ 16X3−12X2−8X+ 3 = 0)m’a donné les quatre racines réelles qui sont :
−1−√13
4,−1−√5 4,−1 + √5 4,−1 + √13 4
Trions un peu, comme cos x∈[−1; 1] on peut éliminer −1−√13
4<−1. Les trois autres sont dans
[−1; 1].−1−√5
4et −1+√5 4sont les valeurs connues respectivement des cosinus des angles 4π 5et 2π 5ce
qui donnerait en degrés α= 72 ou α= 36 ce qui est impossible 1:
2α= 144 =⇒β= 3 ×144 >90. Or nécessairement β < 90. De même :
2α= 72 =⇒β= 3 ×72 >90.
Finalement il ne reste qu’un candidat possible :
cos(x) = −1 + √13
4
Ce qui donne un angle xmesurant environ 49,35˚soit α≃24,68˚
1. Voici le lien avec les triangles d’or qui ont des angles respectifs avec α= 36˚, de (α, α, 3α)et (2α, 2α, α).
http://prof.pantaloni.free.fr 2mail me

http://www.diophante.fr/ D626
3 Construction à la règle et au compas
Le nombre √13 est constructible à la règle et au compas. Par exemple c’est l’hypoténuse d’un
triangle rectangle de côtés 2 et 3 puisque 22+ 32= 13. On construit un tel triangle, on retranche
une unité avec le compas, et on divise le segment restant en quatre (en deux par une médiatrice, puis
encore en deux). On a ainsi construit la longueur −1+√13
4, en rouge sur la figure ci-dessous. Le reste
de la construction se fait alors sans problème.
①J’ai choisi une longueur unitaire pour le côté bleu et j’ai tracé en premier le côté [AH]
②On prend l’écartement −1+√13
4en rouge, et on trace le cercle rouge de centre A.
③Ce cercle coupe [AH]au point I. On trace la perpendiculaire à [AH]en I.
④Cette droite coupe le cercle bleu de centre Aet de rayon AH = 1 en deux points dont le point J.
⑤On construit Lle centre du cercle circonscrit au triangle AHJ .
⑥Maintenant A,H,Jet Lsont construits, on a la longueur orange et les derniers points Met
H′se construisent aisément.
0.5
1.0
1.5
2.0
2.5
3.0
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
A
O
C
D
E
F
G
H
I
J
q
L
uH′
M
http://prof.pantaloni.free.fr 3mail me