DANS L`AIR (BILAN)

Observer
3
C
1. Aperçu historique de la mesure de la vitesse du
Après avoir lu le texte "Aperçu historique" (voir
1.1. P
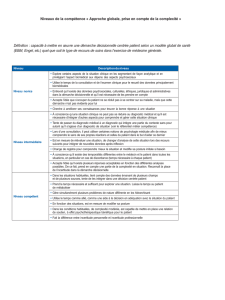
réciser dans le tableau suivant, les paramètres physiques dont dépend ou ne dépend pas la vitesse du son
dans l'air.
La vitesse du son en dépend
Température, pression, taux d’hygrométrie,
vitesse du vent
1.2.
Comment varie la vitesse du son en fonction de la température.
La relation mathématique montre que si T augmente, v augmente.
1.3
. Poser le calcul numérique et donner la valeur de la vitesse du son à la température de
(la masse molaire de l'air étant M = 28,9644 g/mol).
v =  = 
= 346
2. Mesure de la
vitesse du son dans l’air
2.1. Première méthode
d (cm)
10,0 15,0 20,0
τ
(ms)
0,372 0,516
0,635
2.2. Deuxième méthode
x
1
= 23 mm
3. Utilisation des mesures
3.1. Première méthode
3
.1.1. A l’aide du tableur, ajouter une courbe de tendance et faire
afficher son équation et son coefficient de détermination R².
équation : d = 337×t – 0,0
278
3
.1.2. Si besoin est, refaire le même travail après avoir supprimé les
points constituants manifestement des erreurs de mesures.
équation : d = 341×t – 0,0
287
Le coefficient de détermination R²
l'ajustement des estimations de l'équation de régression (modèle
choisi) ; en régression simple, u
n R² proche de 1 est suffisant pour
dire que l'ajustement est bon.
Après avoir éventuellement éliminé quelques points, on obtient un R² satisfaisant : le
modèle est bien ajusté aux résultats expérimentaux.
3.1.3. Reproduire ci-
contre l'allure du graphe.
3.1.4.
Le logiciel propose une équation du type y =ax ou y = ax + b.
A quoi peut correspondre le coefficient directeur "a"
a correspond à une longueur divisée par une durée, c’est une vitesse. C’est la vitesse du son
dans l’air pour l’expérience : v
mesurée
3.1.5. Après la mesure de la température (
Excel). v = 346 m/s
3
.1.6. Comparer à la valeur théorique en calculant l'erreur absolue
U(v) = 346 – 341 = 4 m.s
-1
3
.1.7. En déduire l’erreur relative en %
3.1.8. Identifier les sources d’erreurs.
•
erreur systématique sur la position de l'émetteur et du récepteur
•
incertitude sur la mesure de
•
choix des points "éliminés"
•
On néglige les temps de réponse et d’émission des émetteurs et récepteurs
• Vitesse du son
sans tenir compte de la pression
DANS L ’A IR (B ILAN )
1. Aperçu historique de la mesure de la vitesse du
son
Après avoir lu le texte "Aperçu historique" (voir
ENT
) répondre aux questions suivantes
réciser dans le tableau suivant, les paramètres physiques dont dépend ou ne dépend pas la vitesse du son
La vitesse du son en dépend
La vitesse
du son n’en dépend pas
Température, pression, taux d’hygrométrie,
L’intensité du son
Comment varie la vitesse du son en fonction de la température.
Argumenter
La relation mathématique montre que si T augmente, v augmente.
. Poser le calcul numérique et donner la valeur de la vitesse du son à la température de
(la masse molaire de l'air étant M = 28,9644 g/mol).
= 346
m.s
-1
vitesse du son dans l’air
25,0 30,0 35,0 40,0
45,0
0,635
0,818 1,10 1,14 1,26
1,39
x
2
= 149
mm
.1.1. A l’aide du tableur, ajouter une courbe de tendance et faire
afficher son équation et son coefficient de détermination R².
278
R² = 0,9876
.1.2. Si besoin est, refaire le même travail après avoir supprimé les
points constituants manifestement des erreurs de mesures.
287
R² = 0,9979
Le coefficient de détermination R²
mesure la qualité de
l'ajustement des estimations de l'équation de régression (modèle
n R² proche de 1 est suffisant pour
Après avoir éventuellement éliminé quelques points, on obtient un R² satisfaisant : le
modèle est bien ajusté aux résultats expérimentaux.
contre l'allure du graphe.
Le logiciel propose une équation du type y =ax ou y = ax + b.
A quoi peut correspondre le coefficient directeur "a"
? (on pourra s’aider des unités)
a correspond à une longueur divisée par une durée, c’est une vitesse. C’est la vitesse du son
mesurée
= 341 m.s
-1
3.1.5. Après la mesure de la température (
θ = …… °C) donner la vitesse du son dans l’air (en utilisant le fichier
.1.6. Comparer à la valeur théorique en calculant l'erreur absolue
u(v) = 
.1.7. En déduire l’erreur relative en %
:
!"#$%"
&
'(")%*+$"
'(")%*+$"
4 /345 = 0,01 soit 1
%
erreur systématique sur la position de l'émetteur et du récepteur
incertitude sur la mesure de
∆
t (salves), de d (distance), de la température
choix des points "éliminés"
On néglige les temps de réponse et d’émission des émetteurs et récepteurs
sans tenir compte de la pression
P et de l’hygrométrie
0,1
0,2
0,3
0,4
0,5
0,6
0,0005
) répondre aux questions suivantes
:
réciser dans le tableau suivant, les paramètres physiques dont dépend ou ne dépend pas la vitesse du son
du son n’en dépend pas
. Poser le calcul numérique et donner la valeur de la vitesse du son à la température de
25°C,
45,0
50,0 55,0
1,39
1,58 1,66
mm
Après avoir éventuellement éliminé quelques points, on obtient un R² satisfaisant : le
a correspond à une longueur divisée par une durée, c’est une vitesse. C’est la vitesse du son
= …… °C) donner la vitesse du son dans l’air (en utilisant le fichier
,-./0
%
t (salves), de d (distance), de la température
On néglige les temps de réponse et d’émission des émetteurs et récepteurs
0,001 0,0015
3.2. Deuxième méthode
Détermination de la longueur d’onde
3.2.1. Déduire des mesures la valeur y = 1
2
 1
3
= 15×λ.
y = 4
44
4
5
55
5
– 4
44
4
5
55
5
= 126 mm.
3.2.2. Utiliser cette valeur pour calculer la longueur d’onde λ.
λ = 678
678678
6789
99
9::::;:<=
;:<=;:<=
;:<=>
>>
>::::??
????
??
3.2.3. Pourquoi avoir réalisé une mesure sur 15 longueurs d'onde plutôt qu'une ?
L'incertitude absolue est la même quelque soit la mesure mais l’incertitude relative est plus
faible sur une mesure de grande valeur
3.2.4. A partir de la relation entre λ , la célérité v de l’onde et sa fréquence f déduire la valeur v
mesurée
de la vitesse
du son.
v
mes
= λ×f donc : v
mes
= 8,40×10
-3
×40,0×10
3
soit : v
mes
= 336 m.s
-1
3.2.5. En déduire l’erreur relative : 
!"#$%"
&
'(")%*+$"
'(")%*+$"
Erreur relative : (346 – 336)/346 = 0,03 soit 3 %
3.2.6. Identifier les sources d’erreurs.
• incertitude sur la valeur des abscisses x
1
et x
2
• Incertitude sur l’appréciation des courbes en phase
• Incertitude sur la valeur de la fréquence GBF (voir appareil)
Calculs d’incertitudes
3.2.6. Compte tenu des défauts du dispositif utilisé (fixation des émetteurs et récepteur, décalage du repère …)
l’incertitude sur la position (mesure de x), U(x), est (choisir la réponse qui semble la plus adaptée) :
± 1 mm ±
±±
± 3 mm ± 5 mm ± 1 cm
3.2.7. En utilisant ce qui précède redonner les positions x
1
et x
2
sous la forme (x ± U(x)) :
x
1
= (23 ± 3)mm x
2
= (149 ± 3)mm
3.2.8. Calculer l'incertitude:@A sur la mesure de 15 λ . (on donne : B6²;B1
8
²CB1
5
²:)
si u(x) = 3 mm, alors u(y) = 5 mm
3.2.9. En déduire l'incertitude relative
DE
E
;
DF
F
en %.
U(y)/y = 5/126 = 0,04 soit 4% donc U(λ)/λ = 0,04
3.2.10. Calculer l'incertitude absolue U(λ).
U(λ) = 0,04×λ = 0,04×8,40 = 0,4 mm
3.2.11. Exprimer la valeur de λ sous la forme λ:G:Bλ:H: λ = ( 8,40 ± 0,4 ) mm
3.2.12. En admettant que l'incertitude sur la valeur de la fréquence du GBF est négligeable devant celle de
la longueur d'onde, on peut écrire que l'incertitude relative sur la mesure de la vitesse du son est telle que :
D 
;
Dλ
λ
.
Comparer l'incertitude relative à l'erreur relative de la mesure de la vitesse du son pour cette expérience.
U(v)/v = 0,04 donc : U(v) = 0,04×v = 0,06×336 = 14 m.s
-1
v = (336 ±
±±
± 14) m.s
-1
L’incertitude relative (voir 3.2.9) : 4 % > erreur relative (voir 3.2.5) : 3 %
le domaine d'incertitude contient la valeur de référence, la mesure est cohérente
Remarques :
L’erreur relative – quotient de l’erreur absolue par la "vraie" valeur – indique la qualité du résultat obtenu.
Elle s’exprime généralement en pour cent. Le mot «erreur» est en relation avec quelque chose de juste ou de vrai.
On ne parle d’erreur que si une valeur de référence considérée comme "vraie" est donnée (ici la vitesse du son en
fonction de la température).
Pour la plupart des mesures il n’y a pas à disposition de valeur de référence (la "vraie" valeur de la grandeur
mesurée). On parle alors d’incertitude. L’incertitude absolue résulte toujours d’une estimation. Elle dépend non
seulement des moyens utilisés mais aussi du jugement que porte l’expérimentateur sur ces moyens L’indication
complète du résultat d’une mesure comporte donc la valeur estimée la plus probable (issue de la mesure) et
l’intervalle à l’intérieur duquel se trouve avec un bon niveau de certitude (95% par exemple) la «vraie» valeur
(l’incertitude absolue est la moitié de cet intervalle).
La qualité – ou précision – d’une mesure est donnée par l’incertitude relative. C’est le quotient de l’incertitude
absolue par la grandeur mesurée.