CINÉMATIQUE

CINÉMATIQUE
1 Ballon de football
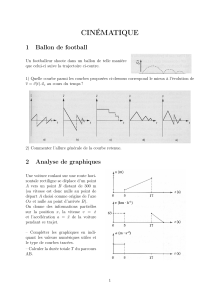
Un footballeur shoote dans un ballon de telle manière
que celui-ci suive la trajectoire ci-contre.
1) Quelle courbe parmi les courbes proposées ci-dessous correspond le mieux à l’évolution de
v=~v(t).~uzau cours du temps ?
2) Commenter l’allure générale de la courbe retenue.
2 Analyse de graphiques
Une voiture roulant sur une route hori-
zontale rectiligne se déplace d’un point
Avers un point Bdistant de 300 m
(sa vitesse est donc nulle au point de
départ Achoisi comme origine de l’axe
Ox et nulle au point d’arrivée B).
On donne des informations partielles
sur la position x, la vitesse v= ˙x
et l’accélération a= ¨xde la voiture
pendant ce trajet.
– Compléter les graphiques en indi-
quant les valeurs numériques utiles et
le type de courbes tracées.
– Calculer la durée totale Tdu parcours
AB.
1

3 Évaluation d’une accélération
Dans un article de Pour la science 1, on s’intéresse aux accéléromètres placés sur une commande
de jeu vidéo. Il y est écrit : "Elle mesure précisément les accélérations de la poignée jusqu’à
des valeurs atteignant trois fois l’accélération de la pesanteur. Des mouvements très rapides
de la main sont ainsi enregistrés, car un aller-retour d’une main sur un mètre en une seconde
correspond à une accélération d’environ 2g."
Pouvez-vous, à l’aide d’un modèle simple, retrouver la valeur de 2gavancée dans l’article ?
4 Parcours nautique
À l’origine des temps, les deux navires (A)d’Arsène et (B)de Bastien sont situés sur un
même méridien ; Aest au nord de Bà la distance d. On assimilera localement la surface de
la Terre à un plan.
1) Bse dirige vers le nord à la vitesse constante VBalors que Ase dirige vers l’est à la vitesse
constante VA. Quelle sera la distance minimale entre les deux navires ?
A.N : d= 10 km ; VB= 36 km/h ; VA= 27 km/h.
2) Aest animé du même mouvement que précédemment. Quel cap (direction) devra prendre
Bpour rejoindre Aen ligne droite ? Quelle sera la durée de son trajet ?
5 Spirale logarithmique
L’équation horaire du mouvement plan d’un point en polaire est la suivante :
r=b e−t
τet θ=ωt avec b, ω et τconstants
1) Calculer les vecteurs vitesse et accélération de ce point.
2) En déduire leur norme.
3) Déterminer l’angle entre le vecteur position et le vecteur vitesse à tout instant.
6 Trajectoire cycloïdale
Une roue de rayon ret de centre Croule sans glisser sur l’axe Ox en restant dans le plan
(Oxz). Soit Mun point lié à la roue, situé sur la circonférence. À l’instant t= 0,Mest
confondu avec l’origine O. La vitesse de Cest constante et égale à v.
z
x
O
θ
C
Μ
1. Jean-Michel Courty, Édouard Kierlik, Accéléromètres en mission, Pour la Science, Juillet 2007
2

1) Exprimer mathématiquement la condition de roulement sans glissement de la roue.
2) Déterminer à l’instant t:
a) la position de M;
b) le vecteur vitesse −→ vde Mdans le référentiel lié à Oxz.
c) le vecteur accélération −→ ade Mdans ce même référentiel.
3) Déterminer −→ vet −→ alorsque Mest en contact avec l’axe Ox.
7 Recherche de la trajectoire la plus rapide
Un homme est sur la plage en un point Aet se propose d’atteindre le plus rapidement possible
un point Bimmobile situé dans l’eau, AB n’étant pas perpendiculaire au bord de mer. Sa-
chant qu’il décrit une trajectoire rectiligne sur la plage à vitesse v1et une trajectoire rectiligne
dans l’eau à la vitesse v2, ces trajectoires faisant des angles i1et i2avec la normale au bord
de mer, déterminer la relation entre i1,i2,v1et v2pour que la durée du trajet soit minimum.
La relation trouvée correspond-elle à celle de l’optique ?
A
B
i
i
1
2
Réponse : v2sin i1=v1sin i2
8 Coordonnées sphériques : calcul du plus court chemin
Sur une sphère de rayon R, le grand cercle (c’est à dire un cercle de rayon Ret de centre, le
centre de la sphère) est le plus court chemin entre deux points.
λétant la latitude et ψla longitude, déterminer la longueur du plus court chemin entre Paris
(λ1= 48o520N ; ψ1= 2o200E) et Tokyo (λ2= 35o420N ; ψ1= 139o300E).
Donnée : rayon terrestre : (6,37 ±0,01).106m (la Terre n’est pas rigoureusement sphérique).
3

9 Mouvement d’une tige
Le système représenté sur la figure ci-dessous est en
mouvement dans le plan (xOy). Il est constitué de deux
roues tournant dans le sens trigonométrique à la vitesse
angulaire ωautour de leurs axes respectifs (O1, ~uz)et
(O2, ~uz), reliées par une tige Tde longueur `, de centre
C. Les axes sont fixes et les liaison en Aet Bsont
articulées. On donne O1A=O2B=a. À t= 0, les
vecteurs −−→ O1Aet −−→ O2Bfont le même angle θ0avec ~ux. Le
référentiel d’étude est R(O, ~ux, ~uy, ~uz).
Quelle est la nature du mouvement de la tige [AB]? Re-
présenter graphiquement et déterminer les expressions
de ~vA/R,~vB/Ret ~vC/R.
10 Saisons terrestres
Quelle caractéristique du mouvement de la Terre par rapport au Soleil est à l’origine des
saisons.
11 Face cachée de la Lune
Dans le référentiel géocentrique, la Lune effectue une ré-
volution circulaire centrée sur la Terre en 27,3jours. La
distance du centre de la Terre au centre de la Lune est
environ égale à DT L = 3,84.105km. Au cours de cette
révolution, la Lune montre toujours la même face à la
Terre.
1) Décrire le mouvement de la Lune dans le référentiel
géocentrique. On s’attachera particulièrement à distin-
guer s’il s’agit d’un mouvement de translation circulaire
ou de rotation.
2) En déduire la vitesse angulaire ˙ θ0de révolution de
centre du la Lune sur sa trajectoire.
3) Déterminer la vitesse et l’accélération du centre de la
Lune sur sa trajectoire géocentrique. Calculer numéri-
quement la norme de sa vitesse.
4) Décrire le mouvement de la Lune dans le repère sélé-
nocentrique qui a ses axes parallèles à ceux du référentiel
géocentrique mais qui a pour origine Lle centre de la
Lune.
5) Déterminer la vitesse angulaire ˙ θPde rotation de la
Lune sur elle-même.
4