tg5 : pyramide et cône

TG5 : PYRAMIDE ET CÔNE
I) Pyramide
a) Pyramide quelconque
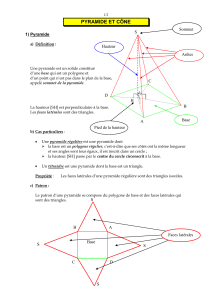
Une PYRAMIDE est un solide composé :
- d’une BASE de forme polygonale,
- de FACES LATÉRALES triangulaires ayant un sommet commun : le SOMMET de la
pyramide.
Remarque : la droite (SH)
perpendiculaire au plan de base
est la HAUTEUR de la pyramide.
b) Pyramide régulière
Une pyramide de sommet S est dite RÉGULIÈRE lorsque :
- sa base est un polygone régulier (côtés et angles égaux) de centre O : triangle
équilatéral, carré…
- [SO] est la hauteur de cette pyramide.
Remarque : les faces latérales d’une pyramide
régulière sont des triangles isocèles
superposables.
c) Patron
Un patron de pyramide se compose du
polygone de base et des faces
latérales triangulaires
Exemple : pyramide régulière à base
carrée.
II) Cône de révolution
a) Définition
Un CÔNE DE RÉVOLUTION est un solide composé :
- d’une BASE constituée d’un disque de centre O,
- d’une SURFACE LATÉRALE en forme de secteur circulaire de sommet S
(voir patron du b))
Le segment [SO] est la HAUTEUR du cône.

Remarque : ce cône est engendré par la rotation du triangle SOM
rectangle en O autour de la droite [SO]. L’hypoténuse [SM] est une
GÉNÉRATRICE de ce cône.
b) Patron
Un patron de cône se compose
de sa base (disque) et de sa
surface latérale (secteur
circulaire)
Remarque : la longueur de l’arc
A
1
A
2
est égale au périmètre
du disque de base.
Exemple : construire le patron d’un cône ayant une base de 3 cm de rayon et dont la génératrice
mesure 8 cm.
- on calcule le périmètre du disque de base : P = 2 × π × r
P = 2 × π × 3 = 6π cm
- on calcule l’angle S du secteur circulaire : il est proportionnel à la longueur de l’arc.
L’égalité des produits en croix donne : x × 16π = 360 × 6π
x = 360 × 6π
16π = 135°
III) Volume de la pyramide et du cône
V = 1
3 × aire de base × hauteur = 1 3 ×
B × h
ou
B = aire du polygone de base
(exemple : B = L × l pour une pyramide à
base rectangulaire)
B = aire du disque de base
B = π × r
2
(où r = rayon du disque de base)
exemples de calculs de volumes
1) calculer le volume d’une pyramide de 15 cm de
hauteur ayant une base carrée de 6 cm de
côté.
B = c
2
= 6
2
= 36 cm
2
V = 1
3 ×
B × h = 1
3 × 36 × 15 = 36 × 15 3 = 180 cm
3
2) calculer le volume d’un cône de 15 cm de
hauteur et de rayon de base 3 cm (on
donnera la valeur exacte puis la valeur
arrondie au mm
3
près)
B = π × r
2
= π × 3
2
= π × 9 = 9π cm
2
V = 1
3 × 9π × 15 = 9π × 15 3 = 45π cm
3
V ≈ 141,372 cm
3
au mm
3
près par excès
Angle en degrés
x
360
Longueur de l’arc en cm 6π 2 × π × 8 = 16π
Périmètre du disque de rayon 8 cm
dont on ne construit qu’un secteur