I- PYRAMIDE QUELCONQUE Une pyramide quelconque est un

Géométrie 2 – PYRAMIDES ET CÔNES
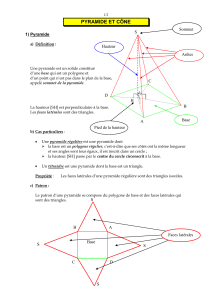
I- PYRAMIDE QUELCONQUE
¾
Une pyramide quelconque est un solide
ayant pour base un polygone dont
chaque sommet est relié à un point
situé en dehors de la base. Ce point est
appelé sommet de la pyramide.
¾
Les faces latérales d’une pyramide sont
triangulaires.
coller ici la photocopie (9 cm)
¾
La hauteur d’une pyramide est la
distance entre son sommet et sa base.
¾
La hauteur d’une pyramide est
perpendiculaire à sa base.
¾
Un tétraèdre est une pyramide à base
triangulaire.
II- PYRAMIDES RÉGULIÈRES
¾
Une pyramide est régulière si :
♦ sa base est un polygone régulier

♦ la hauteur issue du sommet passe par
le centre du cercle circonscrit de la
base.
coller ici les photocopies
¾
Dans une pyramide régulière, les
arêtes latérales sont de même longueur
et par conséquent les faces latérales sont
égales.
¾
Un tétraèdre est régulier si toutes ses
faces sont des triangles équilatéraux ;
toutes les arêtes sont alors égales.
III- PYRAMIDE DONT UNE ARÊTE
LATÉRALE EST PERPENDICULAIRE
A LA BASE
Si une arête latérale est perpendiculaire à
la base d’une pyramide, alors c’est la
hauteur du solide.
coller ici la photocopie

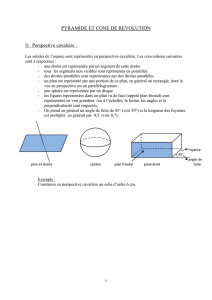
IV- CÔNE DE RÉVOLUTION
¾
Dans un patron de cône, la longueur de
l’arc de cercle de la surface latérale est
égale au périmètre du disque de base.
coller ici la photocopie
¾
Dans un cône de révolution, la hauteur
a pour extrémités le sommet et le
centre du disque de base. Elle est
perpendiculaire à sa base et donc à tous
les rayons du disque de base.
V- AIRE – PYRAMIDE – CÔNE
1. Pyramide
¾
La surface latérale d’une pyramide
est la somme de toutes les surfaces de
ses faces latérales.
¾
La surface totale d’une pyramide est
la somme de sa surface latérale et de
sa base.

2. Cône
¾
La surface latérale d’un cône est celle
de sa partie non plane.
¾
La surface totale d’un cône est la
somme de sa surface latérale et de sa
base (disque).
VI- VOLUME – PYRAMIDE – CÔNE
Le volume d’une pyramide ou d’un cône
est égal au tiers du produit de la surface
de base par la hauteur.
V = Sb × H
3 (Sb = Surface de base et
H = Hauteur du solide)
♦ Si la hauteur du solide (H) est
exprimée en m, la surface de base
(Sb) doit être exprimée en m2.
♦ Ne pas confondre la hauteur du
solide avec la hauteur d’une face
latérale ou celle de la base si c’est
un triangle par exemple.